Использование систем отслеживания истинности предположений для диагностирования на основе моделей
Если устройство состоит из n компонентов, то теоретически может существовать 2" комбинаций отказов компонентов. Решетка вариантов сред является перечислимым множеством присоединений: элемент с наименьшим номером соответствует отсутствию отказов в компонентах, а элемент с наибольшим номером – отказу всех компонентов устройства. Каждая такая среда называется кандидатом, т.е. гипотезой о том, что именно произошло в неисправном устройстве. Вся решетка сред при такой постановке проблемы будет представлять собой пространство кандидатов.
Если устройство работает нормально, то гипотеза, соответствующая кандидату' с наименьшим номером, прекрасно "объясняет" наблюдаемую ситуацию. Если наблюдаются какие-либо отклонения от нормального функционирования устройства, то наблюдаемые проявления можно считать свидетельствами в пользу той или иной гипотезы в пространстве кандидатов. Поскольку объем этого пространства связан с количеством компонентов в анализируемых устройствах экспоненциальной зависимостью, необходимо использовать в нем какой-либо метод эффективного поиска кандидатов.
Ключевым понятием для такого метода должно быть конфликтующее множество – множество таких компонентов, которые в данной ситуации (т.е. при данных симптомах) не могут одновременно быть исправными. Конфликтующее множество, таким образом, это именно то множество допущений, которое в системе отслеживания истинности предположений, основанной на анализе допущений, формирует среды, несовместимые с данными. Их можно определить, формируя дедуктивное замкнутое выражение для среды и данных, а затем выискивая в нем противоречие. Главная цель системы отслеживания истинности предположений состоит при этом в том, чтобы идентифицировать все минимальные конфликтующие множества. После этого можно определить минимальное множество отказавших компонентов, которое объяснит все наблюдаемые проявления ненормальной работы устройства.
В качестве простого примера рассмотрим решетку сред, представленную на рис. 19.6. В этой решетке C1, C2 и С3– компоненты анализируемого устройства. Пусть S – множество наблюдаемых проявлений ненормальной работы этого устройства. Предположим, нам известно, что если наблюдается множество проявлений S, то С1 и С2 не могут быть исправными одновременно, а также С1 и С3. Тогда можно выделить среды, помеченные на схеме решетки значками 0, С2 и С3 (они выделены на схеме как несовместные). Каждая из этих сред имеет какое-либо запрещенное сочетание исправных компонентов. Все другие среды являются кандидатами в пространстве гипотез, но очевидно, что минимальные множества среди них – {С1} и {С2, С3}.
В системе отслеживания истинности предположений используется несколько стратегий управления обработкой пространства кандидатов, например:
- стратегия, основанная на предоставлении преимущества тем гипотезам, которые поясняются проще всего; поиск решения начинается с минимальных по объему (количеству элементов) конфликтных множеств;
- сохранение в системе просмотренной цепочки логического вывода, что позволяет исключить ее повторный просмотр.
В системе GDE также используется мера неопределенности, основанная на теоретико-информационном подходе, с помощью которой выясняется, какие измерения следует выполнить в анализируемой системе. Наилучшей полагается такая измерительная процедура, которая минимизирует энтропию (см. об этом в главе 20), т.е. та, которая вносит наибольшее разнообразие в набор значений вероятностей кандидатов. Предполагается, что априорная вероятность отказа отдельных компонентов известна и что отказы компонентов в вероятностном смысле независимы. Эти же вероятности используются при определении порядка формирования гипотез-кандидатов.
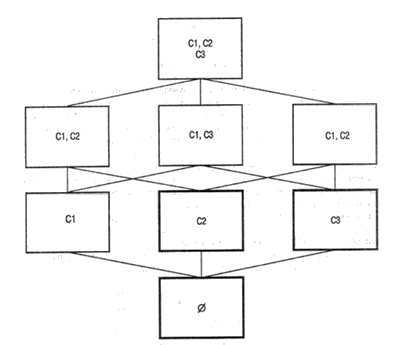
Рис. 19.6. Решетка сред, представляющая пространство кандидатов. Несовместные контексты выделены утолщенным контуром, а минимальные кандидаты заштрихованы