Реализация численных методов
Интерполяция по общей формуле Лагранжа
В этом пакете рассматриваются функции одной переменной вида у(х), как правило, заданные в табличном виде, т. е. рядом значений х и соответствующих им значений у. Именно так обычно задаются данные эксперимента, получаемые на различных физических или электронных измерительных установках.
Важной задачей математической обработки подобных данных является и их представление в виде некоторой математической зависимости, допускающей проведение над нею обычных математических операций, например вычисление у(х) при х, не совпадающих с исходными (узловыми) точками, интегрирование или дифференцирование функций, проведение их статистической обработки (сглаживания или фильтрации) и т. д.
Одной из самых распространенных задач такого рода является интерполяция таблично заданных функций, т. е. вычисление их значений в промежутках между узловыми точками. В математической литературе общепринято представление многих специальных функций в виде математических таблиц, ориентированных на интерполяцию по заданному числу узловых точек (обычно от 2 до 6).
В систему MathCAD встроены функции линейной и сплайн-интерполяции, при которых отдельно на каждом промежутке функция представляется отрезком прямой или кубическим многочленом. Последний вычисляется так, чтобы обеспечить стыковку в узловых точках как значений функции, так и ее первых двух производных (что и дает необходимую гладкость графика функции).
Эти мощные средства интерполяции имеют, однако, существенный недостаток: параметры интерполирующей функции различны на различных участках интерполяции. Другими словами, такая интерполяция не может быть сведена к одной интерполирующей формуле, что затрудняет интерполяцию математических таблиц, за исключением линейной интерполяции, дающей довольно низкую точность.
На рис. 14.14 представлен документ, задающий обобщенную формулу интерполяции методом Лагранжа. Эта формула синтезирует полином Лагранжа, используя два вектора: с координатами xi и yi узловых точек. Преимущества такого подхода в том, что число узловых точек и их расположение может быть любым (в том числе неравномерным), а для интерполяции используется единая интерполирующая формула f(x), к сожалению, довольно сложная.
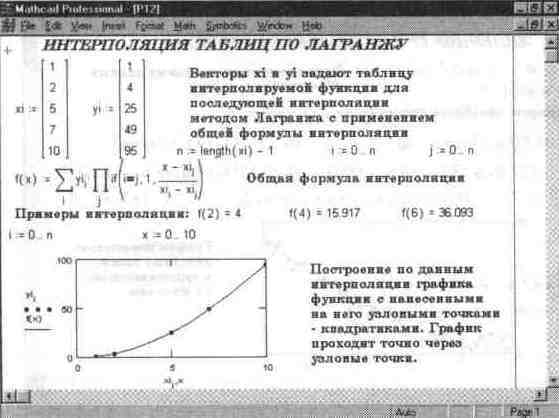
Рис. 14.14. Интерполяция табличных данных по формуле Лагранжа
При интерполяции полиномом Лагранжа степень полинома п однозначно связана с числом узловых точек. Она на единицу меньше этого числа Значения ординат интерполирующей функции в узловых точках совпадают со значениями ординат узловых точек, поэтому график интерполирующей функции f(x) точно проходит через эти точки. К сожалению, при высокой степени полинома (более 5-6) погрешность вычислений его значений заметно возрастает, поэтому выбор n выше 6 на практике нецелесообразен. А это означает, что функция у(х) должна быть представлена небольшим числом достаточно точных значений.
К недостаткам интерполяции по обобщенной формуле Лагранжа относится и довольно большое время вычислений, поскольку формула интерполяции далеко не проста.