Реализация численных методов
Решение дифференциального уравнения первого порядка методом Рунге-Кутта
Решение дифференциальных уравнений широко применяется в практике научно-технических расчетов. Это связано с тем, что дифференциальные уравнения (и системы из них) описывают поведение различных объектов в динамике, например переходные процессы в электронных схемах или работу часового маятника. Линейные дифференциальные уравнения имеют решения в виде специальных функций (скажем, функций Бесселя). Однако многие физические системы нелинейны и описываются нелинейными дифференциальными уравнениями, не имеющими аналитического решения. В этом случае приходится использовать численные методы решения дифференциальных уравнений.
Версия MathCAD 7.0 PRO содержит мощные средства для реализации численных методов решения дифференциальных уравнений. Поэтому может возникнуть вопрос: а нужно ли создавать свои документы для реализации таких методов? Ответ на него не однозначен. Если ваша цель – решение конкретной задачи, то проще воспользоваться готовыми функциями MathCAD. Они были описаны выше. Однако нередко педагоги и специалисты без должных оснований говорят о трудности реализации в системе MathCAD обычных численных методов. Это неверно! Реализация таких методов в системе MathCAD легка и наглядна. Более того, она позволяет вмешиваться в алгоритмическую реализацию методов решения, что способствует созданию новых или улучшенных методов решения дифференциальных уравнений, ориентированных на решение интересующих пользователя задач.
Здесь мы остановимся на реализации решения дифференциального уравнения i/=f(x,y) хорошо известным методом Рунге-Кутта. Пусть h – шаг приращения переменной х, i – индекс, имеющий значения от 1 до N (N – число интервалов решения с шагом h). Метод Рунге-Кутта четвертого порядка дает погрешность решения порядка h(4, что удовлетворяет самым придирчивым требованиям к точности численных методов. Он неоднократно подробно описывался в соответствующей литературе. Его реализация показана на рис. 14.16.
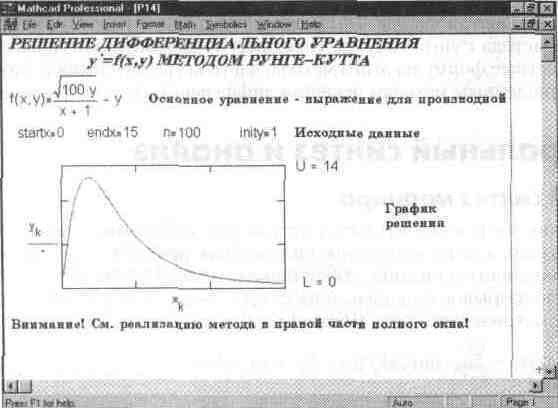
Рис. 14.16. Начало документа, иллюстрирующего решение дифференциального уравнения методом Рунге-Кутта
Документ на рис. 14.16 состоит из двух частей. Первая часть (она и показана на рисунке) содержит ввод исходных данных и вывод графика решения. Для решения надо задать функцию f(x,y), начальное (startx) и конечное (endx) значения х, число точек решения п и начальное значение (inity) переменной у. При построении графика функции указываются нижний (L) и верхний (U) пределы изменения искомой зависимости у(х).
Вторая часть документа (см. рис. 14.17) в действительности располагается справа от первой части и размещается в обычно невидимой части документа. Поэтому пользователь избавлен от созерцания тривиальных или просто не интересующих его математических формул и может сосредоточить внимание лишь на вводе исходных данных и функции f(x,y) и выводе результатов.
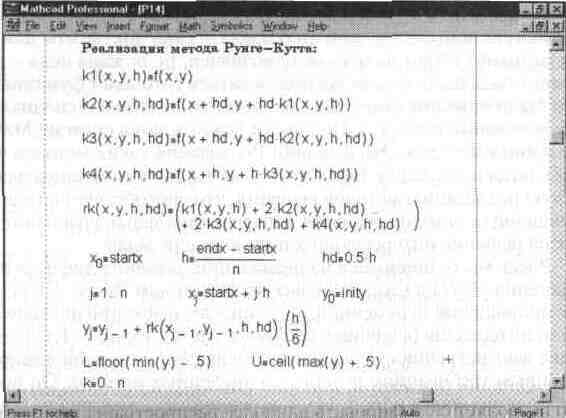
Рис. 14.17. Конец документа, иллюстрирующего решение дифференциального уравнения методом Рунге-Кутта
Рассматривая рис. 14.17, нетрудно сделать вывод о наглядности реализации метода Рунге-Кутта. По существу приведенные уравнения повторяют известные формулы этого метода часто встречающиеся в учебной литературе по численным методам решения дифференциальных уравнений.