Спектральный синтез и анализ
Гармонический синтез пилообразных колебаний
В литературе можно найти множество примеров разложения в ряд Фурье самых разнообразных зависимостей y(t) Используя приведенные для них значения коэффициентов Фурье, можно синтезировать самые разнообразные зависимости (сигналы).
Еще одним примером может служить показанный на рис. 14.19 гармонический синтез треугольных колебаний.
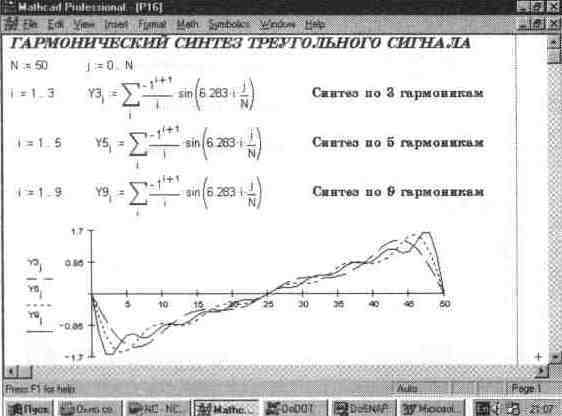
Рис. 14.19. Гармонический синтез треугольных колебаний
Может возникнуть вполне закономерный вопрос зачем столь сложным способом синтезировать такие простые зависимости, если они легко описываются целиком или по частям с помощью простых аналитических выражений? Действительно, если нужно просто смоделировать сигнал как временную функцию, нет необходимости синтезировать его по множеству гармоник.
Однако существует большое количество теоретических методов анализа сигналов и практических устройств, основанных именно на спектральном подходе. Примером могут служить частотные фильтры и даже целые радиотехнические системы. При их анализе сигнал y(t) часто приходится разлагать в ряд Фурье для проведения в дальнейшем операций с гармониками. Имея сигнал y(t) уже в виде гармоник, можно заметно сократить время обработки сигнала и вообще убрать этап задания функции в виде временной зависимости.
Во многих странах до сих пор выпускаются синтезаторы сложных колебаний, основанные на суммировании их гармонических составляющих с разными амплитудой и фазой.
