Реализация численных методов
Линейное сглаживание по пяти точкам
Один из полезных видов статистической обработки функции у(х), заданной п точками, заключается в статистической обработке каждой точки с учетом положения нескольких ближайших точек. Например, простейший способ такой обработки усредняет значения этой точки и нескольких других, окружающих ее слева и справа. В результате будет получен вектор сглаженных значений у(х). Некоторую проблему представляет вычисление сглаженных значений точек, примыкающих к концевым, но можно вывести формулы сглаживания и для этих точек.
MathCAD 7.0 PRO имеет встроенную функцию сглаживания Однако полезно проверить работу известных алгоритмов сглаживания по ряду точек. Так, линейное сглаживание по пяти точкам демонстрирует документ, показанный на рис. 14.15. На нем вначале задан вектор параболической зависимости, на которую наложены сильные случайные компоненты, создаваемые генератором случайных чисел. Далее заданы пять формул сглаживания: по две для крайних двух точек слева и справа и одна для других (эта формула просто находит среднее значение для центральной точки и окружающих ее четырех ближайших точек). Фактически кривая сглаживания состоит из ряда отрезков прямых линий, откуда и название – линейное сглаживание.
На приведенном рисунке видно, что сглаженная кривая проходит внутри облака точек и неплохо вписывается в него. При этом число сглаженных точек равно числу исходных точек (в нашем случае их 50). Разумеется, при таком большом числе сглаженных точек эффективность сглаживания оказывается заметно ниже, чем, например, при проведении регрессии с большим числом исходных точек.
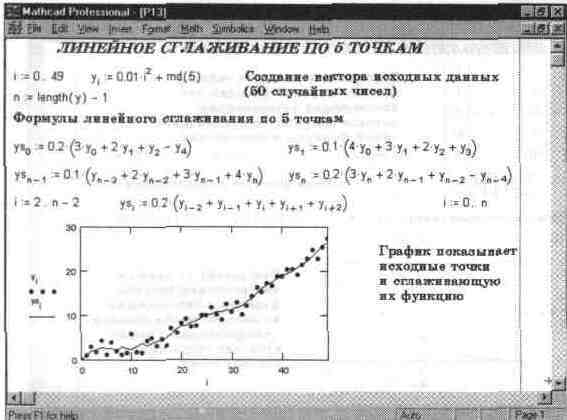
Рис. 14.15. Линейное сглаживание по пяти точкам
Можно повысить эффективность сглаживания, увеличивая число точек, используемых для статистической обработки заданной точки, и перейдя к кривой сглаживания в виде отрезка полинома более высокой степени, чем 1. Так, известны формулы нелинейного сглаживания по семи точкам. Этих формул семь по три для крайних точек и одна для остальных. Для нелинейных зависимостей, близких к параболическим или содержащих отрезки парабол, нелинейное сглаживание гораздо более эффективно, чем линейное. Тем не менее и здесь гладкость кривой сглаживания невелика.
Единого мнения о целесообразности повторения процедуры сглаживания у математиков нет. Одни считают, что повторное сглаживание делает кривую сглаживания более плавной. Другие не рекомендуют применение повторного сглаживания. В целом сглаживание – эффективный инструмент предварительной обработки исходных данных. Затем можно использовать более тонкие методы их обработки, например фильтрацию на основе спектрального анализа и синтеза, полиномиальную регрессию с применением полинома определенного порядка и т. д.
