Спектральный синтез и анализ
Гармонический синтез меандра
Одним из фундаментальных положений математики, ранее казавшимся абстрактным а затем нашедшим широчайшее практическое применение, является возможность описания любой периодической функции, имеющей конечное число разрывов и непрерывность производных между ними, с помощью тригонометрического ряда Фурье:
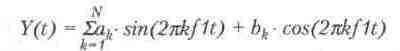
…где k – порядковый номер гармоники, f1 – частота колебания. Этот ряд содержит бесконечное число косинусных и синусных составляющих – гармоник, причем амплитуды этих составляющих а^ и b^ являются коэффициентами Фурье, определяемыми приводимыми несколько позднее интегральными выражениями.
Приведенный ряд содержит бесконечное число членов и при таком представлении оказывается бесполезным, поскольку время вычисления в этом случае также равно бесконечности. К счастью, амплитуды гармоник для реальных зависимостей y(t) довольно быстро уменьшаются по мере роста номера гармоники k. Поэтому на практике обычно приходится иметь дело с ограниченными по числу гармоник рядами Фурье.
Помимо упомянутой формы ряд Фурье можно представить в виде:
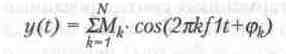
…где амплитуда гармоник М^ и их фаза (р^ определяются выражениями:
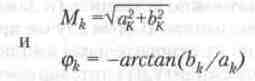
Преимущество ряда в этой форме в том, что для вычисления каждого члена ряда нужно лишь один раз обращаться к довольно медленному вычислению тригонометрической функции. В дальнейшем будут приведены формулы, позволяющие вычислять коэффициенты Фурье (либо амплитуды и фазы гармоник) для любой функции y(t). Это является задачей спектрального анализа. Здесь же мы рассмотрим обратную задачу – синтеза зависимости y(t) путем вычисления ряда Фурье с ограниченным числом членов.
Теория спектрального анализа и синтеза хорошо развита, и для многих зависимостей y(t) заведомо известны значения коэффициентов Фурье или законы изменения (с частотой или номером гармоники) амплитуд и фаз гармоник. Это позволяет синтезировать наиболее распространенные зависимости y(t).
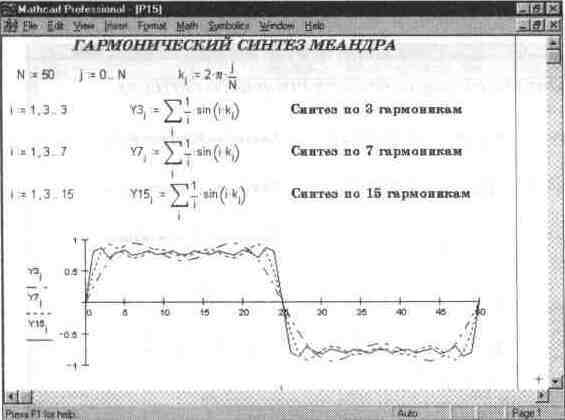
Рис. 14.18. Гармонический синтез меандра
Документ, представленный на рис. 14.18, реализует синтез периодических прямоугольных импульсов со скважностью, равной 2 (меандра). Ряд Фурье для таких импульсов содержит только синусные члены, причем лишь с нечетными k. Это упрощает синтез, который в документе реализован для 3, 7 и 15 гармоник.
Меандр – не самая удачная для синтеза зависимость, поскольку он содержит резкие скачки. Для не очень сведущего в математике пользователя удивительно, что такого рода зависимость вообще синтезируется из синусоид, которые представляют собою гладкие функции без всяких скачков Естественно, что для получения скачков нужно брать очень большое число гармоник Тем не менее уже при 15 гармониках синтезированный сигнал напоминает меандр и отличается от него конечным временем перепада и характерной волнистостью Она усиливается после быстрых перепадов и является проявлением так называемого эффекта Гиббса.
Эффект Гиббса, к сожалению, невозможно устранить (и даже ослабить) лишь увеличением числа гармоник при синтезе В этом случае просто возрастает частота волнообразных колебаний, но их относительная амплитуда меняется незначительно – она доходит до 18% от амплитуды синтезируемых колебаний.
Эффект Гиббса – явление крайне нежелательное Он фактически вводит в синтезируемые колебания новые компоненты, на деле отсутствующие Это может замаскировать или сильно исказить компоненты колебания, которые интересуют исследователя. Поэтому обычно стремятся ослабить эффект Гиббса, даже за счет уменьшения точности синтеза. В дальнейшем будут обстоятельно рассмотрены приемы ослабления этого эффекта.