Графы, деревья и сети
Следующее определение сети более близко к специфике задач искусственного интеллекта, которыми мы сейчас занимаемся.
Определение 6.3
Если L – это множество взвешенных связей, a N, как и ранее, множество узлов, то сеть – это любое подмножество NxLxN, в котором имеет значение порядок в триадах.
Связи в сети практически всегда являются ориентированными, поскольку отношения, представленные взвешенными связями, не должны быть симметричными.
Обыкновенные графы используются для представления взаимоотношений между объектами в пространстве или во времени. Можно использовать их и для представления более абстрактных причинно-следственных связей, как, например, связей между различными видами патологий в медицине (рис. 6.2). Доступ к такой информации связан в той или иной мере с использованием специальных средств прослеживания путей на графе, для которых разработаны самые различные алгоритмы (см., например, работу [Pearl, 1984]).
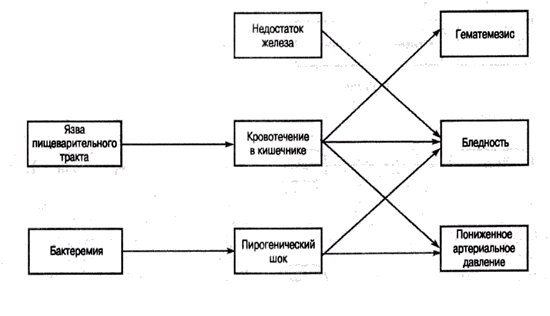
Рис. 6.2. Участок сети причинно-следственных связей [Pople, 1982P]
Для представления иерархических классификаций и сетей применяются деревья. Например, на рис. 6.3 показано дерево классификации болезней по расположению пораженного органа. Корневой узел дерева представляет множество всех болезней, а его наследники – группы болезней, соответствующие основному пораженному органу. Каждый из этих узлов будет иметь своих наследников, представляющих более узкие группы болезней, и т.д. Терминальные узлы дерева будут представлять конкретные заболевания.
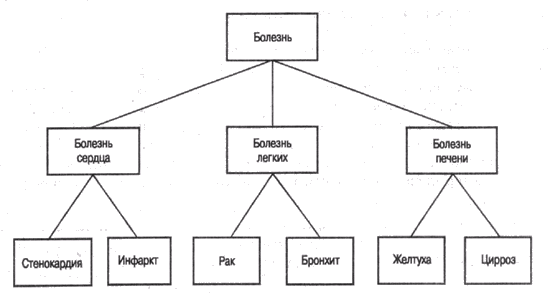
Рис. 6.3. Обыкновенное дерево классификации болезней
