Представление типовых объектов и ситуаций. Основные понятия концепции фреймов.
В этом разделе мы рассмотрим более простой механизм представления знаний, названный системой фреймов. Этот механизм появился в результате стремления объединить декларативные знания об объектах, о событиях и их свойствах и процедурные знания о методах извлечения информации и достижения целей. Предполагалось, что механизм фреймов поможет избежать ряда проблем, связанных с представлением на основе семантических сетей.
Становление теории систем фреймов во многом обязано ряду интуитивных предположений, касающихся механизмов психологической деятельности человека. В частности, предполагается, что представление понятий в мозге не требует строгого формулирования набора свойств, которыми должна обладать та или иная сущность, чтобы можно было рассматривать ее в качестве представителя определенной категории сущностей. Многие из тех категорий, которыми мы пользуемся, не имеют четкого определения, а базируются на довольно расплывчатых понятиях. Создается впечатление, что человек более всего обращает внимание на те бросающиеся в глаза свойства, которые ассоциируются с объектами, наиболее ярко представляющими свой класс.
Такие объекты были названы "прототипическими объектами", или прототипами. В частности, "прототипическая" птица, например воробей, может летать, а потому у нас есть основание полагать, что это – свойство всех птиц, хотя и существуют редкие виды птиц, которые этим свойством не обладают, например пингвины. Именно в этом смысле воробей является лучшим экземпляром категории "птицы", чем пингвин, поскольку он представляет более типические свойства объектов своего класса. Несмотря на существование видов птиц, являющихся исключением в своем классе, мы можем сформулировать обобщенное свойство объектов этого класса следующим образом: "птицы летают".
Теперь обратимся к объектам другого рода– математическим, например многоугольникам. По отношению к этой категории объектов у нас также имеется интуитивное представление о типичности. Например, рассматривая четырехугольники, представленные на рис. 6.5, вряд ли кто будет оспаривать утверждение, что "типичность" объектов увеличивается по мере перехода от фигур, расположенных слева, к фигурам, расположенным справа. Четырехугольник, не обладающий выпуклостью, кажется нам менее типическим, чем выпуклый, а прямоугольник кажется более типическим, чем выпуклый четырехугольник с различными внутренними углами, возможно потому, что площадь фигуры коррелируется в нашем сознании с длиной периметра, а эта связь лучше проявляется при равных значениях внутренних углов.
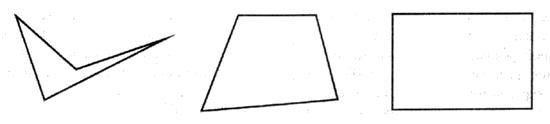
Рис. 6.5. Изменение "типичности" прямоугольников разного вида
В системе фреймов предпринимается попытка судить о классе объектов, используя представление знаний о прототипах, которые хорошо представляют большинство разновидностей объектов данного класса, но должны быть каким-то образом скорректированы, для того чтобы представить всю сложность, присущую реальному миру. Так, если мне ничего не известно о площади более или менее прямоугольного участка земли, но известны длины сторон, то я могу оценить площадь, полагая, что внутренние углы контура этого участка почти равны. В худшем случае, если мои предположения о равенстве углов окажутся уж слишком далеки от действительности, то оценка площади будет завышенной, но такая ситуация типична для подавляющего большинства эвристических механизмов.
При решении практических проблем мы встречаемся с изобилием исключений из правил, а границы между разными классами оказываются очень размытыми. Системы фреймов оказываются полезными по той причине, что они дают нам в руки средства структурирования эвристических знаний, связанных с приложением правил и классификацией объектов. При использовании фреймов эвристические знания не "размазываются" по программному коду приложения, но и не собираются воедино в виде метазнаний, а распределяются между теми видами объектов, к которым они приложимы, и существуют на уровне управления в иерархии представления таких объектов.