Графы, деревья и сети
Следуя Нильсону [Nilsson, 1982], я буду использовать термин структурированный объект по отношению к любой схеме представления, базовые блоки которой аналогичны узлам и дугам в теории графов или слотам и заполнителям структур записей. Я буду систематически сравнивать этот вид представления со схемами, производными от правил формальных грамматик или формализмов разнообразных логик. Представление с помощью структурированных объектов является весьма удобным средством для группирования информации более или менее естественным путем.
В предыдущей главе уже отмечалось, что порождающие правила очень подходят для представления связей состояния некоторой проблемы с действиями, которые необходимо предпринять для продвижения к искомому решению. Однако иногда для решения проблемы больший интерес представляет не ответ на вопрос "Что делать, если…?", а свойства и взаимоотношения между сложными объектами в предметной области. Представлять знания о таких объектах и событиях и их взаимосвязях (таких как тип – подтип, часть – целое, до – после и т.д.) с помощью формальных правил далеко не всегда удобно.
В этой и следующей главах мы рассмотрим способы, удобные для представления структурированных знаний, и остановимся на тех трудностях, с которыми столкнулись исследователи на практике. Формальный аппарат, который будет использован в данной главе, базируется на различных видах графов, узлы которых хранят информацию о сущностях в форме записей, а дуги определяют взаимоотношения между этими сущностями. В следующей главе мы рассмотрим объектно-ориентированный подход к представлению знаний, который влечет за собой определенную методологию разработки и соответствующий стиль программирования.
Для описания многих видов абстрактных данных в информатике вообще и в теории искусственного интеллекта, в частности, очень широко используется терминология, заимствованная из теории графов. Следующие определения приведены здесь для того, чтобы показать, как эти заимствованные термины трактуются при описании структурированных объектов, что несколько отличается от их трактовки в "родной" математической сфере.
Все определения сформулированы в предположении, что существуют два вида примитивов – узлы и связи. Узлы представляют собой исходящие и целевые пункты для связей и обычно каким-либо образом промаркированы. Связи также могут быть промаркированы, но это не обязательно. Все зависит от того, имеем ли мы дело со связями одного вида или разных. В общепринятой терминологии теории графов узлы называются "вершинами", а связи – "ребрами графа", или "дугами".
Определение 6.1
Если N – множество узлов, то любое подмножество NxN является обобщенным графом G. Если в парах подмножества NxN имеет значение порядок, то граф G является ориентированным.
На рис. 6.1 показаны разные типы графов. Обратите внимание на то, что граф не обязательно должен быть связным. Если задаться условием, что петли не допускаются, т.е. в каждой паре должны присутствовать разные узлы, то такой граф называется обыкновенным. Если на графе не допускаются не только петли, но и циклы (т.е. последовательность связей, в которой начальный и конечный узлы совпадают), то такой граф называется лесом.
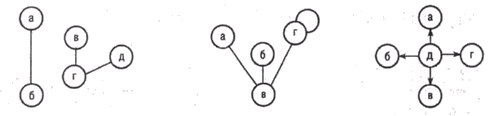
Рис. 6.1. Некоторые виды графов: а) обыкновенный граф; б) связный граф с петлей; в) обыкновенный ориентированный граф – дерево
Определение 6.2
Если G– обыкновенный граф, в котором имеется n узлов и n-1 связей и отсутствуют циклы, то такой граф является деревом.
Иными словами, дерево – это связный лес. Обычно один из узлов дерева является его корнем, например узел е на графе, представленном на рис. 6.1,в. Остальные узлы образуют ветвящуюся структуру "наследников" корневого узла, в которой отсутствуют циклы. Узлы, не имеющие наследников, являются терминальными, или "листьями" дерева, а остальные узлы называются промежуточными (нетерминальными).
В теории графов сетью называется взвешенный ориентированный граф, т.е. граф, в котором каждой связи сопоставлено определенное число. Обычно этими числами оценивается "стоимость" пути вдоль этой связи или длина связи, как на карте дорог. В каждом конкретном случае применения графа как формального средства описания проблемы эти числа могут трактоваться по-своему.