Пространство версий
В этом разделе мы рассмотрим одну из методик обучения, которая получила в литературе наименование пространство версий (version space) [Mitchell, 1978], [Mitchell, 1982], [Mitchell, 1997]. Эта методика была реализована во второй версии системы Meta-DENDRAL. При выводе общего правила масс-спектрометрии из набора примеров, демонстрирующих, как определенные молекулы расщепляются на фрагменты, в этой версии Meta-DENDRAL интенсивно используется механизм обучения концептам, о котором мы рассказывали выше. В работе [Mitchell, 1978] так формулируется проблема обучения концептам.
"Концепт можно представить как образец, который обладает свойствами, общими для всех экземпляров этого концепта. Задача состоит в том, чтобы при заданном языке описания образцов концептов и наличии обучающей выборки – наборе позитивных и негативных экземпляров целевого концепта и способе сопоставления данных из обучающей выборки и гипотез описания концепта – построить описание концепта, совместимого со всеми экземплярами в обучающей выборке".
В этом контексте "совместимость" означает, что сформированное описание должно охватывать все позитивные экземпляры и не охватывать ни один негативный экземпляр.
Для того чтобы "рассуждать" о правилах, касающихся масс-спектрометрии, система Meta-DENDRAL должна располагать языком представления концептов и отношений между ними в этой предметной области. В Meta-DENDRAL это объектно-ориентированный язык (см. главу 6), который описывает сеть с помощью узлов и связей между ними. Узлы представляют атомы в структуре молекулы, а связи – химические связи в молекуле. В этом языке некоторый экземпляр в обучающей выборке соответствует образцу в том случае, если сопоставимы все их узлы и связи и удовлетворяются все ограничения, специфицированные в описании образца.
В контексте проблемы обучения концептам пространство версий есть не что иное, как способ представления всех описаний концептов, совместимых в оговоренном выше смысле со всеми экземплярами в обучающей выборке. Главное достоинство использованной Митчеллом (Mitchell) методики представления и обновления пространств версий состоит в том, что версии могут строиться последовательно одна за другой, не оглядываясь на ранее обработанные экземпляры или ранее отвергнутые гипотезы описаний концептов.
Митчелл отыскал ключ к решению проблемы эффективного представления и обновления пространств версий, заметив, что пространство поиска допустимых описаний концептов является избыточным. В частности, он пришел к выводу, что можно выполнить частичное упорядочение образцов, сформированных описаниями концептов. Самым важным является отношение "более специфичный чем или равный", которое формулируется следующим образом.
"Образец Р1 более специфичен или равен образцу Р2 (это записывается в форме Р2 =< Р2) тогда и только тогда, когда Р1 сопоставим с подмножеством всех образцов, с которыми сопоставим образец Р2".
Рассмотрим следующий простой пример из обучающей программы для "мира блоков" [Winston, 1975, а]. На рис. 20.1 образец Р1 более специфичен, чем образец Р2, поскольку ограничения, специфицированные в образце Р1, удовлетворяются только в том случае, если удовлетворяются более слабые ограничения, специфицированные в образце Р2. Можно посмотреть на эту пару образцов и с другой точки зрения: если в некотором экземпляре удовлетворяются ограничения, специфицированные в образце Р1, то обязательно удовлетворяются и условия, специфицированные в образце Р2, но не наоборот.
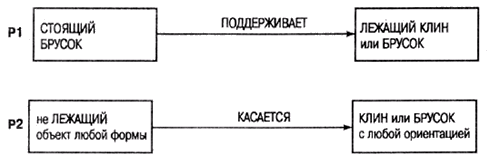
Рис. 20.1. Отношения между образцами
Обратите внимание на следующий нюанс. Для того чтобы программа смогла выполнить упорядочение представленных образцов, она должна быть способна разобраться в смысле множества понятий и отношений между ними, которые специфичны для данной предметной области.
- Программа должна понимать, что если В – это "брусок", то, значит, В – это одновременно и "объект произвольной формы", т.е. в программу должны быть заложены определенные критерии, которые помогут ей выделить категории сущностей, представленных узлами в языке описания структуры образцов.
- Программа должна знать, что если А "поддерживает" В, то, следовательно, А "касается" В в мире блоков, т.е. программа должна обладать способностью разобраться в избыточности отношений между объектами в предметной области.
- Программа должна понимать логический смысл таких терминов, как "не", "любой" и "или", и то как они влияют на ограничения или разрешения в процессе сопоставления образцов.
Все эти знания необходимы программе для того, чтобы она смогла сопоставить образец Р1 с Р2, т.е. узлы и связи в одном образце с узлами и связями в другом, и выяснить, что любое ограничение, специфицированное в Р1, является более жестким, более специфичным, чем соответствующее ему ограничение в образце Р2. Если программа сможет во всем этом разобраться, то открывается путь к представлению пространств версий в терминах большей "специфичности" или большей "общности" образцов в этом пространстве. Тогда программа может рассматривать некоторое пространство версий как содержащее:
- множество максимально специфических образцов;
- множество максимально обобщенных образцов;
- все описания концептов, которые находятся между этими двумя крайними множествами.
Все это в совокупности называется представлением пространств версий граничными множествами (boundary sets). Такое представление, во-первых, компактно, а во-вторых, легко обновляется. Оно компактно, поскольку не хранит в явном виде все описания концептов в данном пространстве. Его легко обновлять, так как определение нового пространства можно выполнить перемещением одной или обеих границ.