Строим икосаэдр
Точное вычисление нормалей
Проверьте результат и обсудите качество. В данном варианте нормали в вершинах заданы так, как будто изображаемой фигурой является сфера, а не икосаэдр. Это достаточно грубое приближение. Если поверхность произвольного вида составлена из треугольников, то вектор нормали к поверхности каждого из них можно вычислить точно, опираясь на данные о координатах вершин треугольника.
Из курса векторной алгебры вы, вероятно, помните, что векторное произведение двух векторов а и b определяется как вектор n, перпендикулярный к плоскости, в которой лежат исходные векторы. Величина его равна площади параллелограмма, построенного на векторах а и b как на сторонах, а направление определяется так, что векторы a, b и п образуют правую тройку. Последнее означает, что если представить наблюдателя на конце вектора п, то он видит поворот вектора а к вектору b, совершаемый по кратчайшему пути против часовой стрелки. На рис. 6.4. изображена нормаль n (правая тройка) при различной ориентации перемножаемых векторов а и b.
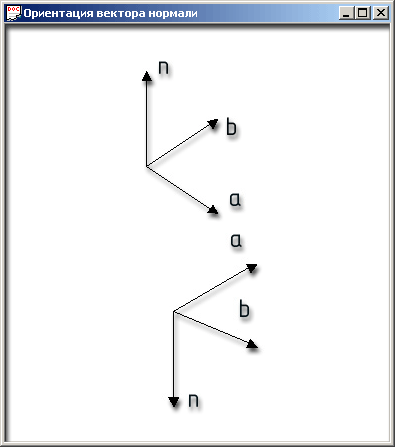
Рис. 6.2. Ориентация вектора нормали
Если координаты векторов а и b известны, то координаты нормали вычисляю по следующим формулам. Длина вектора нормали n зависит от длин вектор сомножителей и величины угла между ними:
Nx=AxBz-AzBy Ny=AzBx-AxBz Nz=AxBy-AyBx
Примечание
Можно потерять много времени на осознание того факта, что не только правление нормали, но и ее модуль влияют на величину освещенности вершины, так как сопровождающая документация (Help) не содержит явных указаний на это. Отметьте также, что цвета вершин полигона влияют на цвета точек заполнения полигона, так как цвета вновь генерируемых тонов интерполируются, то есть принимают промежуточные значения между значениями цвета вершин.
