Классический период: игры и доказательство теорем. Поиск в пространстве состояний.
Для любого данного узла N алгоритм поиска в глубину строит потомок этого узла, т.е. формирует состояние, которое образуется в результате применения операторов к узлу N, а потом переходит к формированию узла, ближайшего к N, на том же уровне графа ("соседу" N), т.е. формирует состояние, которое образуется в результате применения оператора к узлу-родителю N. Алгоритм поиска в ширину действует наоборот – сначала формируются все "соседи" узла N, а потом уже строятся его потомки.
Таким образом, в алгоритме поиска в ширину просматриваются последовательно состояния, представленные узлами одного и того же уровня на графе (рис. 2.2), а в алгоритме поиска в глубину просматриваются состояния на одном пути, а затем происходит возврат назад на один уровень и формируется следующий путь (рис. 2.3).
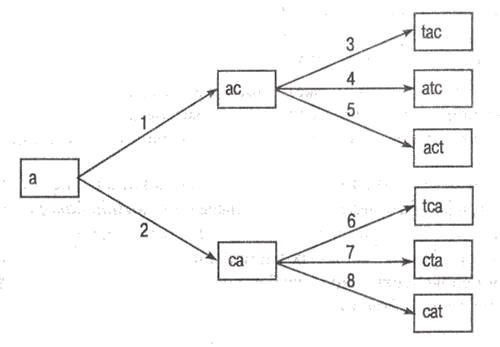
Рис. 2.2. Граф пространства состояний при использовании алгоритма поиска в ширину
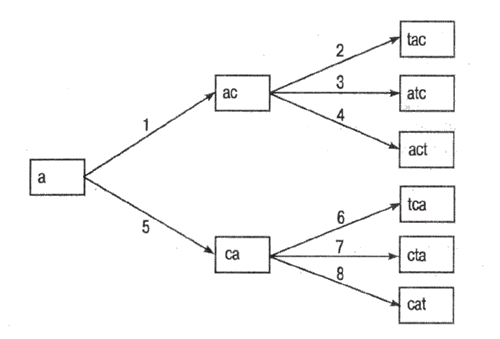
Рис. 2.3. Граф пространства состояний при использовании алгоритма поиска в глубину
На обоих рисунках числа на дугах графа указывают номер шага, на котором формируется тот узел (состояние), для которого эта дуга является входящей. Конечно, этот номер еще зависит и от того, в каком порядке используются операторы из имеющегося множества. В представленном примере сначала применяется оператор, добавляющий очередную букву в конец последовательности, затем оператор, добавляющий букву на предпоследнюю позицию, и т.д., а последним применяется оператор, добавляющий букву на первое место. Но ведь можно использовать и обратный порядок применения операторов.
Оба алгоритма завершат работу (найдут конечное состояние) после формирования узла "act", а не "cat". Но алгоритму поиска в ширину придется для этого "посетить" пять узлов (сформировать и проанализировать пять состояний), а алгоритму поиска в глубину – четыре.
Отметим, что свойства этих алгоритмов существенно отличаются.
- Алгоритм поиска в ширину отыскивает решение, путь к которому на графе – кратчайший, если таковое существует. Другими словами, он находит кратчайший путь между исходным состоянием и решением. Алгоритмы, обладающие таким свойством, называются разрешимыми (admissible).
- Алгоритм поиска в глубину может быстрее найти решение, особенно, если при его выполнении используются эвристики для выбора очередной ветви. Но этот алгоритм может никогда не закончиться, если пространство состояний бесконечно.
