Классический период: игры и доказательство теорем. Поиск в пространстве состояний.
Исследования в области искусственного интеллекта начались практически сразу же после появления компьютеров и первых опытов по их применению для других, более "приземленных" целей. Все началось с того, что вскоре после окончания Второй мировой войны были предприняты попытки решать с помощью компьютера игровые задачи и головоломки. Однако сейчас, оглядываясь назад, можно проследить, как некоторые идеи и подходы к решению проблем с помощью компьютера выросли именно из этих первых экспериментов.
Фундаментальная идея, которая появилась в результате этих первых опытов, получила наименование поиск в пространстве состояний. По существу, идея очень проста. Множество проблем можно сформулировать в терминах трех важнейших ингредиентов:
- исходное состояние проблемы, например исходное состояние головоломки;
- тест завершения – проверка, достигнуто ли требуемое конечное состояние или найдено решение проблемы (примером может послужить правило определения, собрана ли головоломка);
- множество операций, которые можно использовать для изменения текущего состояния проблемы, например шаги или перемещения фигур при сборке головоломки.
Один из способов представления такого концептуального пространства состояний – граф, в котором состояниям соответствуют узлы, а операциям – дуги. Рассмотрим в качестве примера задачу построения слова из некоторого множества букв, как в игре Scrabble. Задавшись набором операций установки букв, можно сформировать пространство состояний.
Предположим, что множество доступных букв включает Т, С и А. На каждом уровне графа мы будем добавлять по одной определенной букве. Каждая ветвь, исходящая из узла, соответствует установке буквы в определенную позицию в последовательности, а эта последовательность должна образовать осмысленное слово (рис. 2.1). Если это произошло, то головоломка считается собранной (например, если образовалась комбинация "act" или "cat"). (Сейчас мы не будем стремиться собрать какое-нибудь сложное слово вроде "scrabble", которое может принести играющему больше очков.)
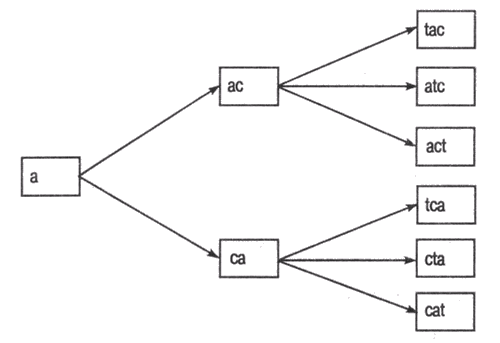
Рис. 2.1. Дерево пространства состояний головоломки Scrabble с буквами Т, С и А
Это пространство состояний обладает двумя интересными свойствами, которые присущи далеко не всем пространствам состояний:
- оно конечно, поскольку существует только п! способов расставить я букв;
- оно не содержит повторяющихся узлов, что может привести к образованию петель на графе.
Метод формирования анаграмм последовательным перечислением является примером применения алгоритма, получившего наименование generate-and-test (порождение и проверка).
- (1) Генерировать новое состояние, модифицируя существующее; например, изменить последовательность букв, добавив новую в существующую последовательность.
- (2) Проверить, не является ли образовавшееся состояние конечным (решением); например, проверить, не является ли образовавшаяся последовательность осмысленным словом. Если это так, то завершить, иначе перейти к шагу (1).
Множество решений, которые удовлетворяют условию на шаге (2), иногда называют пространством решений. В некоторых головоломках, например в уже упомянутой "8 ферзей", решений много, а в других существует всего несколько или только одно. Действительно, существует довольно много способов разместить восемь ферзей на шахматной доске так, чтобы ни один из них не оказался под боем, а вот для головоломки "8-Puzzle" существует единственное решение (см. упр. 7).
Алгоритм имеет два основных варианта: поиск в глубину (depth-first search) и поиск в ширину (breadth-first search). Отличаются варианты порядком формирования состояний на шаге (1). Действительные алгоритмы приведены в упр. 5, а здесь мы дадим только их неформальное описание.
