Опровержение резолюций. Принцип резолюций.
В языке PROLOG используется "интерпретация фраз Хорна для решения проблем" (см. [Kowalski, 1979, р. 88-89]). Фундаментальный метод доказательства теорем, на котором базируется PROLOG, называется опровержением резолюций (resolution refutation). Полное описание этого метода читатель найдет в книге Робинсона [Robinson, 1979], а в этом разделе мы попытаемся кратко изложить только основные идеи.
Ранее я уже вскользь упоминал о том, что мы стараемся упростить синтаксис исчисления таким образом, чтобы уменьшить количество правил влияния, необходимое для доказательства теорем. Вместо дюжины.или более правил, которые используются при доказательстве теорем вручную, системы автоматического доказательства для фразовых форм используют единственное правило вывода – принцип резолюций, – впервые описанное Робинсоном ([Robinson, 1965]).
Рассмотрим следующий пример из исчисления высказываний. В дальнейшем прописными буквами Р, Q, R,… будут обозначаться отдельные фразы, а строчными греческими U, ф и £ – пропозициональные переменные, как и раньше.
Если U и ф представляют две произвольные фразы, которые можно представить в конъюнктивной нормальной форме, и U={ U1,…, Ui,…., Um}, и ф= {ф1…, фi…..,фn}, и Ui, = фi при 1[i[m m,1 [j [ n, то новую фразу £ можно вывести из объединения U' и ф', где: U' = U{ Ui} и ф' = ф{ф,}.
Фраза £ = U' и ф' называется резольвентой шага резолюции, а U и ф являются родительскими фразами. Иногда говорят, что U и ф "сталкиваются" на паре дополняющих литералов Ui, и фj.
Мощность резолюции обеспечивается тем, что в ней суммируется множество других правил. Это станет очевидно после того, как обычные правила будут представлены в конъюнктивной нормальной форме.
В левой колонке табл. 8.1 перечислены наименования правил вывода, в средней показано, как они выглядят в обычных обозначениях, а в правой колонке – во фразовой форме. В каждой записи выражения в верхней части представляют схему предпосылок, а выражения в нижней части – схему заключений. Из этой таблицы видно, что каждое из цитированных выше пяти правил является одним из экземпляров резолюции!
Таблица 8.1. Обобщение резолюции.
| Правило вывода | Обычная форма | Конъюнктивная нормальная форма |
|---|---|---|
| Modus ponens | (U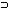 ф,U)/Ф ф,U)/Ф |
{U,Ф},{U}/{ф} |
| Modus fallens | (U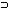 ф.ф)/-U ф.ф)/-U |
{U,ф},{-,ф}/{-U} |
| Сцепление | (U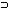 ф,ф ф,ф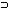 £)(U £)(U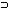 £) £) |
{U,ф},{ф,£}/{U,£} |
| Слияние | (U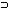 ф,U ф,U 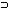 ф)/ф ф)/ф |
{U,ф},{U,ф}/{ф} |
| Reductio | (U,U)/ | | {U},{U}/{} |
Обратите внимание на то, что противоречие в правиле, которое обычно обозначается значком 1, дает в результате пустую фразу – {}. Это означает, что предпосылки несовместимы. Если считать, что предпосылки описывают некоторое состояние предметной области, то такой набор предпосылок не может быть реально обеспечен в ней, т.е. такое состояние невозможно.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Главное, что нужно вынести из всего сказанного выше, что компонент автоматического доказательства теорем, который является основным компонентом большинства систем искусственного интеллекта и, в частности, языков программирования искусственного интеллекта, таких как PROLOG, является системой опровержения резолюций. Для того чтобы доказать, что р следует из некоторого описания состояния (или теории) Т, нужно положить – р и попытаться доказать, что из этого предположения следует утверждение, противоречащее Т. Если это удастся сделать, то тем самым подтверждается утверждение р, а в противном случае оно опровергается.
В исчислении предикатов использование резолюций требует дополнительных усилий, поскольку в этом исчислении присутствуют переменные. Основная операция сопоставления в доказательстве теорем с помощью резолюций называется унификацией (подробное описание используемого при этом алгоритма читатель найдет, например, в работе Нильсона [Nilsson, 1980]). При сопоставлении дополняющих литералов отыскивается такая подстановка переменных, которая превращает оба выражения в идентичные.
Например, выражения БЕЖИТ_БЫСТРЕЕ_ЧЕМ(Х, улитка) и БЕЖИТ_БЫСТРЕЕ _ЧЕМ (черепаха, Y) превращаются в идентичные при подстановке {Х/черепаха, Y/улитка}. Такая подстановка называется унификатором. Наша цель – отыскать наиболее общую подстановку такого рода.
