Дискретизация аналогового сигнала. Разбиение на равные интервалы.
Первое, на что стоит обратить внимание, это – изменение амплитуды вдоль одной оси. Можно условиться, что это ось времени (хотя в принципе это несущественно для абстрактного примера).
Справка
Амплитуда происходит от латинского слова "amplitude", что переводится как "величина" и означает максимальное отклонение изменяющейся по определенному закону величины от среднего значения или от некоторого значения, условно принятого за нулевое.
Разбиение на равные интервалы
В качестве первой операции необходимо разбить эту ось на определенные интервалы, возможно, это и будут интервалы по времени (рис. 6.2).
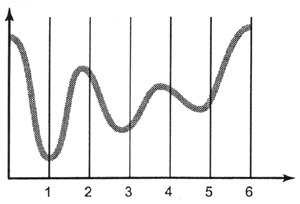
Рис. 6.2. Разбиение аналогового сигнала на интервалы
Цель такого разбиения проста – это единственный способ получения дискретных элементов, причем стоит обратить внимание, что применяется искусственный прием, который ранее мы определяли как "принудительная" дискретизация.
Важная мысль
Для создания дискретных элементов применяется искусственный прием – "принудительная" дискретизация.
В самом деле, выбранные интервалы принципиально никак не учитывают содержание сигнала, а хладнокровно "режут по живому" – в этом суть процесса "принудительной" дискретизации.
В данном конкретном случае дискретизация является линейной, т. к. используется всего одна координата (одна линия, вдоль которой происходит разбиение на равные интервалы).
Замечание
В общем случае интервалы могут быть и разными, но тогда придется ответить на два вопроса: во-первых, как попасть в нужные, смысловые точки, а во-вторых, как передать с каждым дискретным интервалом значения разных длительностей. Не стоит забывать, что все указанные действия ориентированы на техническую реализацию. А техника "склонна" выполнять механические и однозначные действия.
Полученные интервалы очень полезно каким-либо образом "пометить", например пронумеровать с помощью натурального ряда чисел: 0, 1, 2, 3 и т. д.
Можем ли мы считать, что процесс дискретизации закончен? Отнюдь нет. Ведь кривая аналогового сигнала, подвергнутая "принудительной дискретизации", нисколько не изменилась, получить какие бы то ни было элементы пока не удалось.
В самом деле, только количества "дискретов", на которое разделяется сигнал, явно недостаточно. Поскольку в этом случае (по количеству "дискретов") могут казаться равными все сигналы одинаковой длины, ведь они составляются из одинакового количества "дискретных интервалов", хотя внутри интервалов сигналы будут абсолютно разными (рис. 6.3).
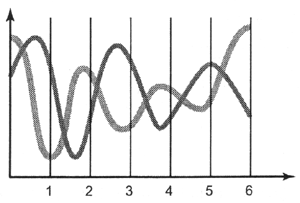
Рис. 6.3. Два разных аналоговых сигнала с одинаковыми интервалами
Пример-метафора
Пока наши действия напоминают работу метронома. Действительно, мы разделили непрерывный сигнал на определенные длительности времени: скажем, каждую секунду происходит биение, и эти биения мы можем пронумеровать и сосчитать. Но то, что происходит между этими биениями, пока выпадает из фиксирования.
А почему? Ответ ясен: дискретные интервалы принципиально ничем не отличаются от сигнала в целом (кроме, разумеется, длительности). Ведь внутри интервалов такой же непрерывный фрагмент аналогового сигнала. В обоих случаях – непрерывные сигналы. И кажется, что решение состоит в уменьшении интервалов.
Замечание
Уменьшение интервалов, конечно, имеет определенное значение, например эта процедура определяет качество цифрового сигнала.
Однако на данном этапе, когда мы рассматриваем логические основания, необходимо понять, что принципиально деление на все более мелкие (до бесконечности) элементы данную проблему не решает.
Вспомним знаменитую апорию древнегреческого философа Зенона об Ахилле: чемпиону по бегу не удается догнать черепаху. Почему? Черепаха вышла, прошла какую-то часть своего пути прежде, чем начнет свой бег спортсмен. Но прежде, чем он пробежит свою половину пути, черепаха сдвинется на какое-то расстояние. И рассуждая строго логически, приходим к выводу, что нельзя догнать эту загадочно-логическую черепаху.
Справка
Апория (от греческого слова "aporia", что означает "безвыходность") – это трудная или неразрешимая проблема, связанная с возникновением противоречия, с наличием аргумента против очевидного и общепринятого. Зенон из Элей (ок. 490-430 до н. э.) – представитель элейской школы, его считают основателем диалектики как искусства постижения истины посредством спора или истолкования противоположных мнений. Философ известен знаменитыми апориями, обосновывающими невозможность движения. Решение апории состоит в исключении бесконечного деления пространства и времени, что в реальной действительности принципиально невозможно.
В самом деле, мы пока не дали ясного ответа на вопрос: зачем было затеяно это деление на дискретные фрагменты?