Дискретизация минимального элемента штрихового изображения
Пример-метафора
Скажем, в понятие качества пищевых продуктов мы вкладываем их вкус, отсутствие вредных примесей и, наоборот, присутствие полезных ингредиентов и прочего.
Поэтому выбор разрешения и определяет взаимосвязь между оригиналом и цифровым изображением, а именно, нужно таким образом определить разрешение, чтобы цифровое изображение соответствовало исходному оригиналу.
Примечание
Впрочем, не факт (мы забегаем вперед), что можно на самом деле получить адекватное качественное изображение на оттиске, даже имея "качественное битовое изображение". Надо понимать, что проблем между входом и выходом еще достаточно много.
Поэтому основное значение разрешения состоит в обеспечении качества изображения. А как следует понимать качество? Разумеется, сугубо метрологически.
Справка
Метрология – это наука об измерениях и методах достижения заранее определенной точности. Ее название происходит от греческих слов "metron", что означает "мера", и "logos" – "слово" или "учение". Эта наука занимается построением общей теории измерений; формированием систем единиц физических величин, разработкой методов измерений, созданием и поддержкой эталонов, проверкой мер и средств измерений. Важнейшими вехами в истории науки и технологии являются установление эталона метра (Франция, конец VIII века), а также разработка и принятие в 1960 году Международной системы единиц (СИ).
С точки зрения метрологии качество понимается как соответствие результата заранее заданному уровню. Так что, если в оригинале имеется минимальная линия определенной толщины, то метрологически качественным будет такое цифровое изображение, которое достоверно отображает эту линию.
Важная мысль
В метрологии качество понимается формально: как соответствие результата заранее заданному уровню.
Разумеется, если известно значение толщины минимального элемента оригинала, можно рассчитать соответствующее разрешение (создать соответствующую сетку дискретизации) и, тем самым, определить требуемый размер пиксела.
Также логично предположить, что если мы так рассчитаем разрешение, что размер стороны пиксела (не забываем, Что пиксел – это "квадратик") будет равен толщине линии, нам удастся однозначно оцифровать такой чертеж (рис. 8.8).
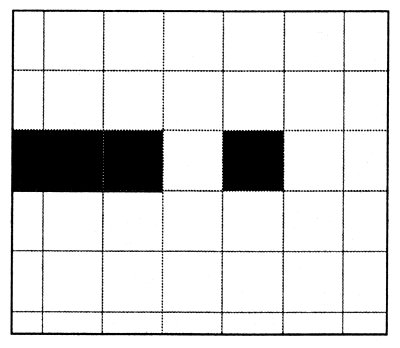
Рис. 8.8. Равные значения высоты пиксела и толщины линии
Таким образом, если высота пиксела оказывается равной (или очень близкой, т. е. в пределах погрешности) минимальному элементу изображения, то мы можем передать такую линию вполне достоверно. А так ли это?
Дело в том, что если посмотреть внимательнее, данный случай напоминает идеальную ситуацию, какая имела место при оцифровке квадрата.
Информацию об "идеальном квадрате" см. в главе 7.