Иллюстрированный самоучитель по Maya 4.5 для начинающих

Катись, мяч, катись!

Теперь можно приступить к качению. Как предотвратить скольжение сферы? Мы заставим ее вращаться внутри группы для создания впечатления качения. Если мы поделим длину кривой на длину окружности сферы, то узнаем, сколько раз ей нужно повернуться вокруг своей оси за время движения по поверхности. Радиус сферы равен 1. Формула вычисления длины окружности следующая:

Итак, длина окружности нашей сферы составляет:

Таким образом, каждый раз, когда сфера преодолеет 6.28 единицы и выполнит один полный оборот, выглядеть это будет так, будто она катится по поверхности, чувствуя трение с ней. Мауа предлагает пару весьма полезных способов для измерения расстояний. Тот, который потребуется нам для измерения длины нерегулярной кривой, называется Arc Length Tool (Длина Дуги).

1. Выберите Create › Arc Length Tool (Создать › Длина Дуги). В режиме Wireframe mode (Режим Каркас) щелкните мышкой по кривой. Инструмент показывает вам расстояние между началом кривой и точкой, на которую вы укажете курсором (рис. 7.7). Перетащите Arc Length Tool (Длина Дуги) в конец кривой и запомните появившееся значение.

   
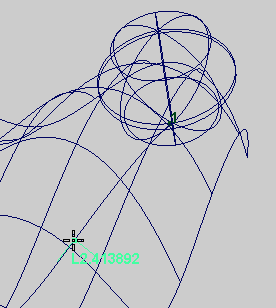
   Рис. 7.7. Инструмент Arc Length Tool (Длина Дуги) измеряет длину дуги между началом кривой и любой точкой на ней

2. Разделите длину кривой на длину окружности сферы, которая составляет 6.28.

   В нашей анимации длина кривой составляет 25.54 единицы.

   25 / 6.28 = 4.07
3. Следовательно, сфера сделает вокруг своей оси 4 полных оборота.
4. Умножьте результат на 360.

Теперь вы знаете, на сколько градусов должна повернуться сфера, чтобы прокатиться по всему пути движения.

1. Идите в начало анимации.
2. Выделите сферу (не группу!) и выберите направление вращения.
3. Задайте ключевой кадр для этого параметра вращения.
4. Идите в конец временной шкалы.
5. В кадре 400 увеличьте значение вращения на число, которое вы получили в результате вычислений, и задайте еще один ключевой кадр (рис. 7.8).
6. Откройте Graph Editor (Редактор Анимационных Кривых) и задайте для касательных вращения сферы тип Linear (Линейный) (рис. 7.9).

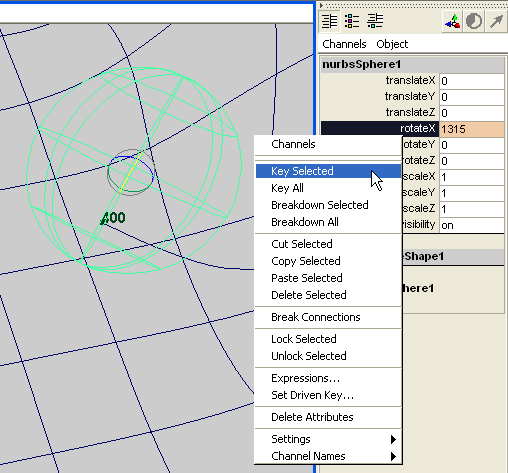
Рис. 7.8. После небольших вычислений вращение сферы получает второй ключевой кадр. В нашем случае она поворачивается на – 1464 градусов вокруг оси Z