Примеры, иллюстрирующие возможности дескрипторной графики
Теперь рассмотрим более сложные примеры, наглядно демонстрирующие возможности дескрипторной графики. Воспользовавшись File › New- > M-File или edit msl.m. создадим файл msl.m следующего содержания:
[x,y] = meshgrid([-2:.4:2]); Z =sin(x. ^ 2+y.^2); fh = figureCPosition.[350 275 400 300].'Color'. V); ah = axes('Color'.[.8.8.8].'XTick'.[-2-1 0 1 2].... 'YTick',[-2-1 0 1 2]}; sh = surfaceCXData.x.'YData'.y.'ZData'.Z.... 'FaceColor',get(ah.'Color')+..... 'EdgeColor'. 'k'.'Marker'.'o'.... 'MarkerFaceColor',[.5 1.85]):В этом файле заданы три объекта: прямоугольник fh – объект класса figure, оси с метками ah – объект класса axes и трехмерная поверхность sh – объект класса surface. Она является результатом наложения объектов fh и ah друг на друга. При этом объект ah класса axes явно наследует свойства объекта fh класса figure. Наследование здесь проявляется в том, что при задании свойства "цвет граней" (FaceColor) объекта sh используется осветление (добавлением константы 0.1) цвета осей, полученного при помощи функции get (ah .color).
Команда view(3) изменяет точку обзора трехмерной поверхности. Раньше, когда параметры осей были жестко заданы, мы смотрели на поверхность строго сверху. Теперь команда view(3) установила точку обзора трехмерных графиков, принятую по умолчанию.
Теперь создадим второй файл – ms2.m:
h(1) = axes('Position',[0 0.1.1); sphere; h(2) = axes('Position'.[0 0.4.6]); peaks: h(3) = axes('Position'.[0.5.5.5]); sphere: h(4) = axes('Position'.[.5 0.4.4]); sphere; h(5) = axes('Position'. [.5 0.50.5.3]): cylinder([0 0 0.5]); set(h,'Visible'.off): alpha(0.1): set(gcf.'Renderer'.'opengl')Здесь задано 5 трехмерных объектов: три сферы разных размеров, поверхность peaks и цилиндр.
Запустив файл ms2, мы получим еще более интересную картину. Заново будет вычислена величина z, а затем построены изображения пяти фигур:
z = 3*(1-x). ^ 2.*exp(-(x. ^ 2) - (y+1). ^ 2)-10*(x/5 -x.'3 -y."5).*exp(-x.^2-y.^2)-1/3*exp(-(x+1).^2 -y.^2)Последовательность наложения фигур, заданных в файле ms2, определяется последовательностью их появления в файле. Любопытен вид цилиндра – похоже, что произошедшее с ним преобразование связано с изменением системы координат с декартовой на сферическую.
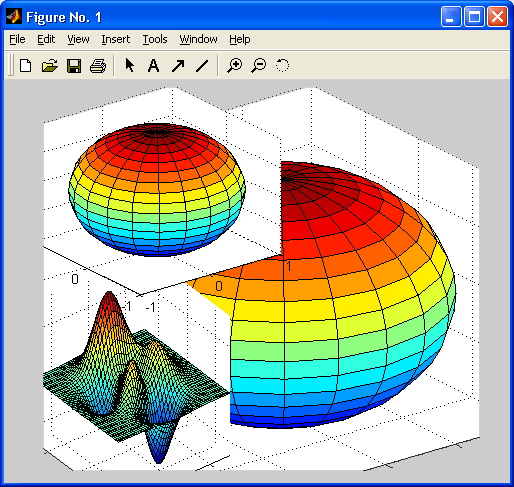
Рис. 7.8. Комбинированный рисунок, полученный при запуске файла ms2.m после запуска ms1.m
Чтобы понять, какие из объектов наследуют свойства других объектов, следует рассмотреть диаграмму иерархии объектов дескрипторной графики MATLAB, что объекты surface расположены ниже объектов axes, а те, в свою очередь, расположены ниже объектов класса figure. Поэтому ясно, что в случае запуска файла msl свойства сетки, построенной с применением объекта axes, будут унаследованы объектом sh, построенным командой surface.
[Обратите внимание, что трехмерная графика в этом примере строится с рендерингом MATLAB 6 ('opengl'). В MATLAB 5.3 без установки патча Open GL по умолчанию был бы выбран рендеринг с использованием Z-буфера и на некоторых компьютерах были бы возможны искажения. Не было бы прозрачной фигуры. В MATLAB 6 при включенном режиме видеоадаптера TrueColor можно пропустить последнюю команду. Но при необходимости вывода изображения на печать set(gcf,'Renderer','opengl') можно быстро отредактировать и заменить на set(gcf,'Renderer', 'painters'). – Примеч. ред.]
Все объекты второго файла – ms2 – относятся к классу axes. Именно поэтому они строятся поверх объектов, показанных на рис. 7.10. Координаты всех пяти трехмерных фигур (см. рис. 7.11) жестко заданы в соответствующих командах axes. В заключение этого раздела следует еще раз отметить, что дескрипторная графика рассчитана не столько на конкретных пользователей, использующих MATLAB как прикладную программу, сколько на опытных разработчиков программного обеспечения для этой системы. Разумеется, это не исключает полезную возможность изменения параметров графиков путем настройки свойств графических объектов, что особенно наглядно видно из последних приведенных примеров. Многие тайны дескрипторной графики познаются только в ходе практических экспериментов с ней.