Графические примитивы
Ну что ж, если все получается, то пора постепенно переходить к более сложным вещам, а именно, к рисованию дуг окружностей и эллипсов. Но прежде следует вспомнить, что в Бейсике используется радианная мера углов (см. "Стандартные функции Бейсика"). Любая дуга имеет угол, от которого она начинается, и угол, где она заканчивается. Чтобы разобраться с этим, сначала я приведу оператор рисования дуг окружностей:
CIRCLE (X, Y), R, С, а, b
Где появившиеся две новые величины а и ь и обозначают эти углы. Правило рисования дуг на Бейсике звучит так: "дуга строится от угла а к углу b против часовой стрелки".
Для того чтобы показать это наглядно, лучше всего обратиться к тригонометрической окружности (рис. 1.18).
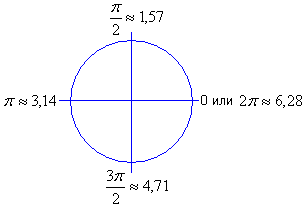
Рис. 1.18. Тригонометрическая окружность
Взглянув на тригонометрическую окружность, мы всегда довольно легко сможем определить начало и конец нужных нам дуг. Более того, Бейсик позволяет использовать в качестве операндов в своих командах арифметические выражения. Поэтому, например, если вы знаете угол начала дуги – 30°, но затрудняетесь определить его на тригонометрической окружности, то можете в соответствующем месте оператора дуги написать:
3.14*30/180
И пусть компьютер сам считает.
Приведем несколько простых примеров.
Построим верхнюю половину окружности синего цвета с радиусом 30 (рис. 1.19), у которой центр находится в точке 150, 100.
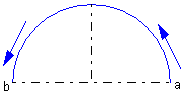
Рис. 1.19. Верхняя половина окружности
Первым делом, глядя на дугу, определяем направление против часовой стрелки. Это дает нам возможность выяснить, где находится начало и конец дуги. Далее обращаемся к тригонометрической окружности. В этом простом примере сразу видно, что угол начала а=0, а угол конца дуги b=3.14. Таким образом, оператор построения этой дуги выглядит так:
CIRCLE (150, 100), 30, 1, 0, 3.14
Построим правую половину той же самой окружности (мы уже не будем сопровождать это построение рисунком, т. к. процесс аналогичен). По тригонометрической окружности определяем, что а=4.71, b=1.57. Записываем оператор построения дуги:
CIRCLE (150, 100), 30, 1, 4.71, 1.57
Предупреждение
Прежде, чем мы приведем более сложный пример дуги, хочется сделать еще одно полезное замечание. Если в операторе построения дуг поставить знак минус перед значениями углов дуги, то автоматически будут проведены радиусы, соединяющие центр окружности с концами дуг. Нельзя ставить минус перед 0. В этом случае вместо нуля надо использовать – 6.28 (т. е. 2я).
