Дифференцирование. Первая производная.
С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, от о-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными. Невозможно дифференцирование функций только вблизи точек их сингулярности.
Вычислительный процессор Mathcad обеспечивает превосходную точность численного дифференцирования. Но больше всего пользователь оценит возможности символьного процессора, который позволяет с легкостью осуществить рутинную работу вычисления производных громоздких функций, поскольку, в отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций.
В Mathcad 11 для ускорения и повышения точности численного дифференцирования функций, заданных аналитически, автоматически задействуется символьный процессор (см. разд. "Оптимизация вычислений"гл. 3).
Первая производная
Для того чтобы продифференцировать функцию f (х) в некоторой точке:
- Определите точку х, в которой будет вычислена производная, например х: = 1.
- Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак ?.
- В появившихся местозаполнителях (рис. 7.3) введите функцию, зависящую от аргумента х, т. е .f(х), и имя самого аргумента х.
- Введите оператор = численного или › символьного вывода для получения ответа.
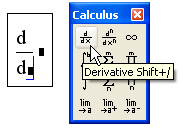
Рис. 7.3. Оператор дифференцирования
Пример дифференцирования функции f(x)=cos(x)ln(x) приведен в листинге 7.10.
Листинг 7.10. Численное и символьное дифференцирование:
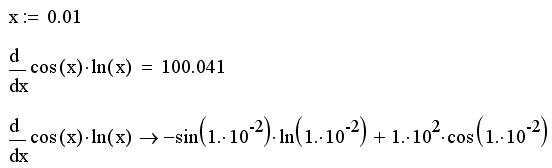
Не забывайте предварительно определять точку, в которой производится численное дифференцирование, как это сделано в первой строке листинга 7.10. Иначе будет выдано сообщение об ошибке, показанное на рис. 7.4, гласящее, что переменная или функция, входящая в выражение, ранее не определена. Между тем, символьное дифференцирование не требует обязательного явного задания точки дифференцирования. В этом случае вместо значения производной (числа или числового выражения) будет выдана аналитическая зависимость (см. верхнюю часть рис. 7.4).

Рис. 7.4. Ошибка в применении оператора дифференцирования
Конечно, можно, как и при использовании других операторов, предварительно определить функцию в отдельном выражении, а затем посчитать ее производную (см. листинг 7.11); или применить оператор дифференцирования для определения собственных функций пользователя (см. листинг 7.12).
