Построение гистограмм
Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы служит функция hist, записываемая в следующем виде:
- N=hist(Y) – возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y – матрица, то выдается массив данных о числе попаданий для каждого из ее столбцов;
- N=hist(Y,M) – аналогична вышерассмотренной, но используется М интервалов (М – скаляр);
- N=hist(Y.X) – возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора X;
- [N,X]=HIST(…) – возвращает числа попаданий в интервалы и данные о центрах интервалов.
Команда hist(…) с синтаксисом, аналогичным приведенному выше, строит график гистограммы. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором х:
>> x=-3:0.2:3; >> y=randn(1000.1); >> hist(y,x) >> h=hist(y.x) h =Columns 1 through 120 0 3 7 8 9 11 23 33 43 57 55Columns 13 through 2470 62 83 87 93 68 70 65 41 35 27 21Columns 25 through 3112 5 6 3 2 1 0Построенная гистограмма показана на рисунке 6.8.
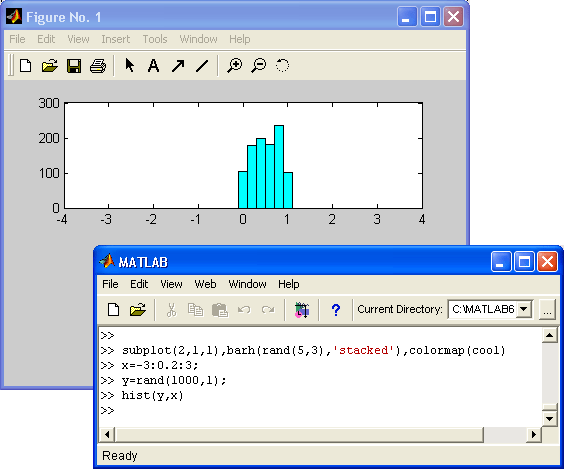
Рис. 6.8. Пример построения гистограммы
Нетрудно заметить, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно наблюдать еще большее соответствие этому закону.
