Создание массивов со случайными элементами
Функция randn генерирует массив со случайными элементами, распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 1:
- randn(n) – возвращает матрицу размера nхn. Если n – не скаляр, то появится сообщение об ошибке;
- randn(m.n) или randn([m n]) – возвращают матрицу размера mxn;
- randn(m,n,p,…) или randn([m n р…]) – возвращает массив с элементами, значения которых распределены по нормальному закону;
- randn(size(A)) – возвращает массив того же размера, что и А, с элементами, распределенными по нормальному закону;
- randn (без аргументов) – возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет нормальное распределение;
- randn('state') – возвращает двухэлементный вектор, включающий текущее состояние нормального генератора. Для изменения состояния генератора можно применять следующие формы этой функции:
- randn('state',s) – устанавливает состояние в s;
- randn('state',0) – сбрасывает генератор в начальное состояние;
- randn('state', j) – для целых j устанавливает генератор в J-e состояние;
- randn('state', sum(100*clock)) – каждый раз сбрасывает генератор в состояние, зависящее от времени.
Пример:
>>Y=randn(4.3) Y =-0.4326-1.1465 0.3273-1.6656 1.1909 0.17460.1253 1.1892-0.18670.2877-0.0376 0.7258Проверить распределение случайных чисел по нормальному закону можно, построив гистограмму распределения большого количества чисел. Например, следующие команды:
>> Y=randn(10000.1); >> hist(Y,100)Строят гистограмму (рис. 10.2) из 100 столбцов для 10 000 случайных чисел с нормальным распределением.
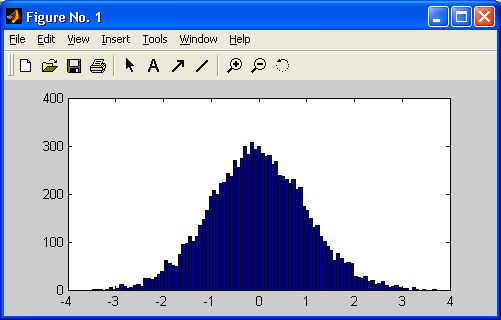
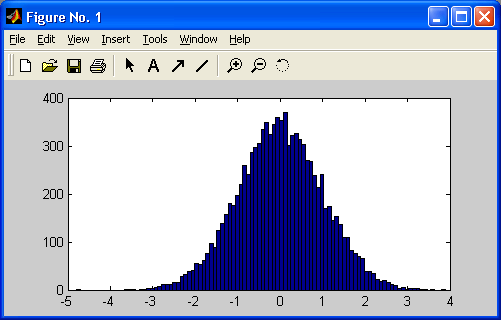
Рис. 10.2. Гистограмма для 10 000 нормально распределенных чисел в 100 интервалах
Из рисунка видно, что огибающая гистограммы действительно близка к нормальному закону распределения.
В пакете расширения Statistics Toolbox можно найти множество статистических функций, в том числе для генерации случайных чисел с различными законами распределения и определения их статистических характеристик.
