Иллюстрированный самоучитель по Mathematica 5

Линейное представление наибольшего общего делителя (функция ExtendedGCD)

Пример 6.9.
Линейное представление наибольшего общего делителя чисел, десятичная запись которых состоит из m единиц и n единиц. Наибольший общий делитель чисел, десятичная запись которых состоит из т единиц и п единиц, является числом того же вида, причем количество единиц в нем равно d = НОД(n, m). Выясним, как он представляется в виде линейной комбинации.

Вот нужные нам определения.

Теперь можно написать и программу:

Заметьте, что десятичная запись чисел r и s в данной таблице содержит только цифры 0 и 1. Я не удивлюсь, если вы предположите, что это связано с наличием некоторых полиномиальных тождеств и потому значения г и s получаются в результате подстановки 10 (основания системы счисления) в них. Например, строку таблицы:

Можно истолковать так:

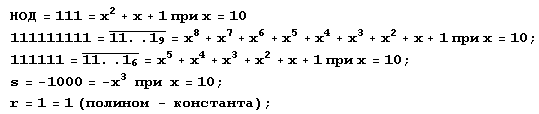
S = -1000 = -x³ при х = 10;
r = 1 = 1(полином-константа); поэтому:

Х² +х + 1 = 1*(x⁸ +х⁷ + х⁶ + х⁵ + х⁴ + х³ +х² +х + 1) + (-x³)-(x⁵ +х⁴ + x³ + х² +х+ 1) при х = 10.

Однако само это равенство выполняется при любом g:, а не только при дс = 10. Значит, в качестве г и s можно взять числа, имеющие точно такое же представление в любой системе счисления, а не только в десятичной! Конечно, наличие строки в таблице еще не означает автоматически тождественную справедливость соответствующего равенства, это лишь означает, что соответствующее равенство справедливо при х = 10. Поэтому вполне возможно, по крайней мере теоретически, что нам просто повезло.

Если говорить честно, так оно и есть. Дело ведь в том, что по равенству d = ra+sb (d = НОД(a, b)) числа r и s определяются неоднозначно: если d = ra+sb, то d = (r+b)a+(s-a)b и d = (r-b)a+(s+a)b. Иными словами, если d = ra+sb, то d= r'a+s'b (при r'= r+b и s' = s-а) и d-r"a+s"b (при r" = r-b и s"= s+d). Так что наличие строки еще не означает наличие тождества. Но, с другой стороны, числа г и s определяются однозначно, если на них наложить ограничения |r <b и |s| <a. Более того, все пары значений г и s можно получить, несколько раз выполняя переход от какой-либо пары фиксированных значений г0 и s0 к новой паре значений по правилам г' = г+b и s'= s-a или r' = r-b и s'= s+a.

Конечно, наличие полиномиальных тождеств сомнений не вызывает, ведь наибольший общий делитель полиномов (х) = x^n-1 + х^n-2 + x^n-3 +… + х +1 и b(х) = х^m-1 +х^m-2 +х^m-3 +… + х+1 равен d(x) = x^d-1 + x^d-2 + х^d-3 +… + х +1, где d = НОД(n,m).

Так как он представим в виде линейной комбинации а(х) -х^n-1 + х^n-2 + х^n-3 +… + х +1 и b(х) = х^m-1 + х^m-2 + х^m-3 +… + х+1, то имеет место равенство d(x) = r(x)a(x)+s(x)b(x). Более того, полиномы г(х) и s(x) можно выбрать так, чтобы deg r(x)<m и deg s(x)<n. Проблема, собственно, состоит вот в чем. По числам а и b мы без труда восстановили полиномы а(х) = x^n-1 + х^n-2 + x^n-3 +… + xⁿ +1 и b(х) =х^n-1 +х^n-2 +х^n-3 +… + х + 1, но можем ли мы так же просто восстановить и полиномы г(х) и 5(х)?

Предположим теперь, что для равенства d = ra+sb (d = НОД(я, b)) с \r\ <b и \s\ <a мы написали равенство полиномов того же типа, что и приведенное выше. Запишем это равенство в виде d(x) = r(x)a(x)+s(x)b(x). Разумеется, здесь а(х) = х^n-1 +х^n-2 +х^n-3 +… + х + 1 и b(х) = x^n-1 +х^n-2 + х^n-3 +… + Х + ].

Поскольку a<b и |s| <a, то deg r(x)<m и deg s(x)<n, а потому правая часть найденного тождества есть полином степени не выше m+n. Тогда, как известно, чтобы проверить написанное равенство, достаточно проверить его при т+п+1 значении х. (Конечно, такую проверку совсем несложно запрограммировать в системе Mathematica.) Но можно поступить и иначе. Достаточно убедиться, что представление г и s будет одинаковым для т+п+1 значений основания системы счисления. (Ведь фактически это будет означать, что равенство полиномов степени не выше m+n выполняется при n+m+1 значении х.) Именно таким способом мы и поступим в следующем примере. (Вопрос о том, есть ли среди найденных представлений такие, которые основаны не на полиномиальных тождествах, намеренно оставляю открытым. Впрочем, вот подсказка: ответ знают некоторые студенты мехмата уже на первом семестре. Я, конечно, совсем не имел в виду, что это написано в учебниках или обязательно излагается на лекциях, но догадаться можно.)