"Наихудшие" случаи для алгоритмов нахождения наибольшего общего делителя
Пример 6.3.
Взаимная простота чисел 2n -1 и 2m -1 при взаимно простых лит. Как известно, числа 2n -1 и 2m -1 взаимно просты, если взаимно просты пит. Выясним, до какого номера n(предполагая, что т<п) система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.
Вот нужная нам функция.
fn[n_] := 2 ^ n - 1Теперь можно написать и программу.
Do[Do[If[GCD[n, m] == 1, If[GCD[fn[n], fn[m]] != 1, Print[n, ":", m]]], {m, n - 1}], {n, 10000}] //TimingДля первой тысячи чисел все проверки на моем весьма слабеньком ПК выполняются всего лишь за 8.125 секунды! Правда, для проверки этого утверждения в пределах первых десяти тысяч чисел понадобится уже 3398.78 секунды. Здесь, очевидно, сказывается не только увеличение и, но и увеличение временных затрат на нахождение наибольшего общего делителя больших чисел.
Пример 6.4.
Наибольший общий делитель чисел, запись которых в десятичной системе состоит из т единиц и n единиц. Как известно, наибольший общий делитель чисел, запись которых в десятичной системе состоит из m единиц и n единиц, является числом того же вида, причем количество единиц в нем равно d= НОД(n, m). Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.
Вот нужные нам определения.
alll[n_] := (10 ^ n - 1) / 9d := GCD[n, m]Теперь можно написать и программу.
Do[Do[If[GCD[alll[n], a111[m]] != alll[d], Print[n, ":", m]], {m, n - 1}], {n, 1000}] //TimingПроверка в пределах первой сотни занимает всего лишь 0.234 секунды, хотя при этом наибольшее число указанного в условии вида имеет 100 цифр! Проверка же в пределах первой тысячи у меня потребовала в 200 раз больше – 46.594 секунды. Чтобы выполнить проверку в пределах первых пяти тысяч, потребуется 6879.67 секунды.
Пример 6.5.
Наибольший общий делитель чисел аn -1 и аm -1. Как известно, наибольший общий делитель чисел аn -1 и аm -1, запись которых в системе счисления с основанием а состоит из n цифр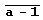 
и из m цифр 
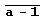является числом того же вида, причем количество цифр й-1 в нем равно d= НОД(n, m). Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.
Вот нужные нам определения.
aaa[a_, n_] := a ^ n - 1; d := GCD[n, m]Теперь можно написать и программу.
Do[Do[Do[If[GCD[aaa[n, a], aaa[m, a]] != aaa[d], Print[n, ":", m]], {m, n - 1}], {n, 100}], {a, 100}] //TimingДля выполнения этой программы потребуется 19.797 секунды. Весьма впечатляющий результат!
Пример 6.6.
Наибольший общий делитель чисел Фибоначчи. Проверим, что наибольший общий делитель n-го и m-го чисел Фибоначчи равен числу Фибоначчи с номером d = НОД(n, m). Иными словами, проверим, что НОД (Fibonacci [n], Fibonacci [m]) = Fibonacci [НОД (n,m) ]. Выясним, сколько времени системе Mathematica понадобится для проверки этого утверждения для n, т, не превосходящих 1000.
Вот нужное нам определение.
d := GCD[n, m]Теперь можно написать и программу.
Do[Do[If[GCD[Fibonacci[n], Fibonacci[m]] != Fibonacci[d], Print[n, ":", m]], {m, n - 1}], {n, 1000}] //TimingДля выполнения этой программы потребуется всего лишь 15.75 секунды.