Линейное представление наибольшего общего делителя (функция ExtendedGCD)
Пример 6.10.
Линейное представление наибольшего общего делителя чисел аn -1 и аm -1. Наибольший общий делитель чисел а" -1 и а" -1, запись которых в системе счисления с основанием а состоит из и цифр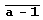 
и из т цифр 
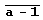, является числом того же вида, причем количество цифр я-1 в нем равно d= НОД(n, m). Выясним, как наибольший общий делитель чисел аn -1 и аm -1 представляется в виде их линейной комбинации.
Вот нужные нам определения.
aaa[a_, n_] := a ^ n - 1; d := GCD[n, m]Теперь можно написать и программу. Нужно только не забыть о том, что представление r и s лучше всего получить в системе счисления с основанием я. Для этого вполне подойдет функция IntegerDigits. Она, правда, теряет знак числа, так что его придется печатать отдельно.
Do[ Do[ Do[ {{g,(r,s}} = ExtendedGCD[aaa[a,n],aaa[a,m]], Print["###", n, ":",m,":",d,":",a,":"], If[g<0,Print["-"]], Print[IntegerDigits[g,a], ":"], If[r<0,Print!"-"]], Print[IntegerDigits[r,a], ":"], If [s<0,Print["-"]], Print[IntegerDigits[s,a]]}, {a,2,n+m+2}],{m,n-1}],{n,10}]Заметьте, что в программе вставлена печать fit для удобства форматирования результатов.
Скажу сразу, что более скучной таблицы я, наверное, никогда не видел! И все из-за удивительного постоянства г и s! Представление r и s выглядит одинаково в системах счисления с разными основаниями, и потому их представления просто повторяются во многих строках! Это значит, что представление наибольшего общего делителя действительно основано на полиномиальных тождествах вида d(x) = r(x)a(x)+s(x)b(x), причем полиномы r(х) и s(x) легко восстанавливаются по числам r и s!
Конечно, я избавлю вас от демонстрации всего этого и просто приведу некоторые наиболее характерные строки таблицы. Разумеется, большинство строк an опустил, и таблица содержит пропуски. Они обозначены строками с многоточиями. Чтобы развеять сомнения, достаточно взглянуть вот на это.
Линейное представление наибольшего общего делителя чисел аn -1 и аm -1:
НОД= r-(an -l) + s-(am -l)
| n | m | d= НОД (n, m) | Основание системы счисления а | Цифры НОД в системе счисления с основанием а | Цифры r в системе счисления с основанием а | Цифры s в системе счисления с основанием а |
|---|---|---|---|---|---|---|
| 2 | 1 | 1 | 2 | (1) | {0} | {1} |
| 2 | 1 | 1 | 3 | {2} | {0} | (1) |
| 2 | 1 | 1 | 4 | {3} | {0} | {1} |
| 2 | 1 | 1 | 5 | (1) | {0} | (1) |
| 3 | 1 | 1 | 2 | {1} | {0} | {1} |
| 3 | 1 | 1 | 3 | {2} | {0} | {1} |
| 3 | 1 | 1 | 4 | {3} | {0} | {1} |
| 3 | 1 | 1 | 5 | {4} | {0} | (1) |
| 3 | 1 | 1 | 6 | (5) | {0} | {1} |
| 3 | 2 | 1 | 2 | (1) | {1} | -{1.0} |
| 3 | 2 | 1 | 3 | (2} | {1} | -{1.0} |
| 3 | 2 | 1 | 4 | (3) | {1} | -{1.0} |
| 3 | 2 | 1 | 5 | (4} | {1} | -{1.0} |
| 3 | 2 | 1 | 6 | (5) | {1} | -{1.0} |
| 3 | 2 | 1 | 7 | (6) | {1} | -{1.0} |