"Наихудшие" случаи для алгоритмов нахождения наибольшего общего делителя
"Наихудшим" случаем для классического алгоритма Евклида нахождения наибольшего общего делителя считается случай соседних чисел Фибоначчи. Чтобы оценить быстродействие, попытаемся, например, определить, при каком n будет заметна задержка при вычислении:
GCD[Fibonacci[n + 2] Fibonacci[n + 1]]Возьмем, например, следующую программу.
Do[Print[n, ":", GCD[Fibonacci[n + 2], Fibonacci[n + 1]]], {n, 10000}]Увы! Алгоритм, реализованный в системе Mathematica, столь эффективен, что даже на весьма посредственном ПК эта программа выполняется без каких бы то ни было задержек.
Если же программу модифицировать так:
Do[Print[n,":",GCD[Fibonacci[2An+2], Fibonacci[2An+1]]],{n,10000}], то задержка будет весьма ощутимой уже при n = 25. Но не забывайте, что 225 + 2 =33554434, а число Fibonacci[2^25+2] имеет 7012462 цифры!
Так что алгоритм, реализованный в системе Mathematica, справляется с классическим "наихудшим" случаем не просто вполне удовлетворительно, а блестяще! Правда, известны алгоритмы, для которых наихудший случай представляют числа u = аn +аn-1, и v= аn-1, где 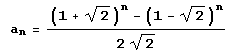 .
.
Давайте исследуем и этот случай. Нам понадобятся следующие определения.
a[n_] := FullSimplify[((1 + Sqrt[2]) ^ n - (1 - Sqrt[2]) ^ n) / (2Sqrt[2])] u := a[n] + a[n - 1] v := a[n - 1]Попытаемся выполнить программу.
Do[Print[n, ":", GCD[u, v]], {n, 100}]Окажется, что уже при n = 98 выражения "не хотят" упрощаться! Поэтому определение а[n_] лучше изменить.
a[n_] := (Expand[(1 + Sqrt[2]) ^ n] - Expand[(1 - Sqrt[2]) ^ n]) / (2 Sqrt[2])Однако при таком подходе понятно, что значительное время тратится также на раскрытие скобок. Однако даже при n = 70 000 вычисления не занимают слишком много времени. При этом значении и числа u и v являются 26 794-значными, и основное время уходит на их вычисление, а не на вычисление их наибольшего общего делителя, который вычисляется в мгновенье ока! Отсюда можем сделать вывод, что функция GCD реализована весьма эффективно, и если при ее использовании возникают неприятности, то, скорее всего, они связаны с вычислением не самой функции, а ее аргументов!
Пример 6.2.
Взаимная простота чисел Ферма. Числа Ферма возрастают довольно быстро и являются взаимно простыми. Поэтому их наибольший общий делитель должен быть равен 1. Выясним, до какого номера n система Mathematica сможет в приемлемое время проверить взаимную простоту этих чисел.
Вот нужная нам функция.
fermat[n_] := 2 ^ (2 ^ n) + 1Теперь можно написать и программу.
Do[Print(n, ":", GCD[fermat[n + 1], fermat[n]]], {n, 100}]Задержка начинает ощущаться при n = 28. Однако вычисления заканчиваются (и притом довольно быстро, если учитывать количество цифр в числах) и при n= 29. Напомню, что уже 22-е число Ферма имеет более миллиона (1 262 612) знаков, а 23-е число Ферма является 2 525 223-значным! Шутки ради 24-е число Ферма, являющееся 5 050 446-значным, я перетащил в Word. Текстовый редактор с записью этого числа работает медленнее, чем система Mathematica! Вот уж воистину супервычислитель: решает задачу быстрее, чем иные успевают произнести ее формулировку! 25-е число Ферма является 10 100 891-значным, и Word его не выносит: замедляется работа меню, даже курсор движется так медленно, что работать становится практически невозможно.
