Иллюстрированный самоучитель по Mathematica 5 › Арифметика: простые числа › Число простых чисел, не превосходящих х [страница - 126] | Самоучители по математическим пакетам

Иллюстрированный самоучитель по Mathematica 5

Число простых чисел, не превосходящих х

Если же построить график на интервале (0, 10000), то графики Иллюстрированный самоучитель по Mathematica 5 › Арифметика: простые числа › Число простых чисел, не превосходящих х и Li(x) практически сольются.

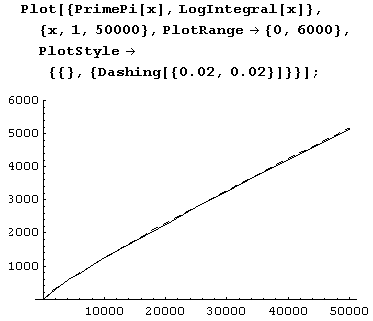
Иллюстрированный самоучитель по Mathematica 5 › Арифметика: простые числа › Число простых чисел, не превосходящих х

Раз уж речь зашла о приближении k(х), давайте построим графики разности функции 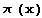Иллюстрированный самоучитель по Mathematica 5 › Арифметика: простые числа › Число простых чисел, не превосходящих х и известных ее аппроксимаций.

В качестве первой (самой простой) аппроксимирующей функции выберем 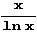Иллюстрированный самоучитель по Mathematica 5 › Арифметика: простые числа › Число простых чисел, не превосходящих х (приближение Чебышева и Лежандра), в качестве второй – 1л(х) (приближение Гаусса), а в качестве третьей – R(x) (приближение Римана).

Сначала определим функцию R(x).

Riemann[x_] := Last[Block[{R = LogIntegral[x], y = LogIntegral[Sqrt[x]] / 2, n = 2},  
{ 
    While[y > 0.000000001, { 
        R = R - y; 
        n = n + l; 
        y = LogIntegral[x ^ (1 / n)] / n 
    }],  
    R 
}]]

Теперь можем построить нужные нам графики.

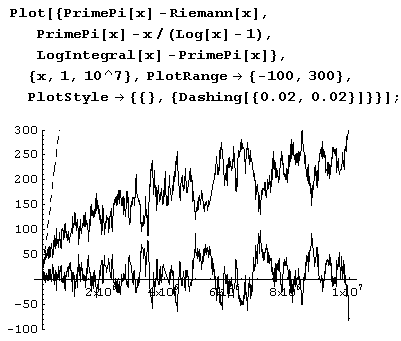
Как видим, из трех наилучшим является приближение Римана. И еще одно замечание. Как мы видели, график функции π(х) выглядит вполне гладко, хотя на самом деле он является ступенчатым. Более того, существуют сколь угодно длинные интервалы, на которых он горизонтален. Однако длина таких интервалов незначительна по сравнению с их расстоянием до начала координат. Это интервалы, на которых функция π(x) не изменяется. Иными словами, это интервалы, на которых нет простых чисел. Кстати, а как сосчитать количество простых чисел на интервале (а, b]?