Поиск отрезков натурального ряда, состоящих только из составных чисел
За одним-единственным исключением pn =2, р2 = 3, числа рn и рn+1 не являются смежными в натуральном ряду. Еще Евклид знал, что существуют сколь угодно длинные отрезки натурального ряда, целиком состоящие из составных чисел. Как же найти отрезок натурального ряда, целиком состоящий из составных чисел? Для этого полезно определить следующую функцию.
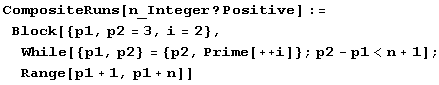
Вот как ее можно использовать.
CompositeRuns/@Range[10]Здесь она запускается 10 раз. Вот что получится (вывод немного отформатирован).
{4}, 8.9}, 8.9.10}, 24.25.26.27}, 24.25.26.27.28}, 90.91.92.93.94.95}, 90.91.92.93.94.95.96}, 114.115.116.117.118.119.120.121}, 114.115.116.117.118.119.120.121.122}, 114.115.116.117.118.119.120.121.122.123}}Как видите, она находит отрезок натурального ряда заданной длины, целиком состоящий из составных чисел. С ее помощью легко найти и отрезок длиной 150, целиком состоящий из составных чисел.

