Иллюстрированный самоучитель по Mathematica 5

Поиск отрезков натурального ряда, состоящих только из составных чисел

Однако полезнее эту функцию модифицировать так, чтобы она выводила на печать только длину отрезка и его начало.

Тогда вывод выглядел бы так (конец обрезан).

Однако среди этой информации все еще слишком много шума. Логично было бы исключить избыточную информацию:

Таблица стала, как видим, значительно компактнее и информативнее. Однако для построения такой таблицы ни функцией CompositeRuns, ни функцией CompositeRunsStart пользоваться не выгодно: обе функции начинают вычисления, не используя уже вычисленных значений, и потому при построении такой таблицы для каждого ее значения начинали бы вычисления с самого начала. Поэтому для построения такой таблицы лучше воспользоваться специальной программой. Для начала подойдет, например, следующая программа.

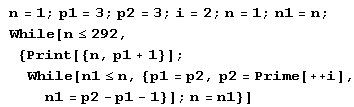
Эта программа выводит список пар. В каждой паре сначала указана длина интервала, а затем – его начало, причем указывается, естественно, начало того ближайшего к началу натурального ряда интервала, который имеет указанную длину. Длина же для данного начала указана наибольшая: она не может быть увеличена, так как следующее за указанным интервалом число – простое. Полученные результаты, весьма нетривиальные, удобно представить в виде таблицы.

Имея такую таблицу, несложно указать и наибольший интервал составных чисел, содержащийся в данном начальном отрезке начального ряда. Однако для этой цели совсем несложно определить функцию, которая все делает автоматически.