Поиск отрезков натурального ряда, состоящих только из составных чисел
У всякой истории есть мораль, и эта не исключение. Некоторые функции, даже если они описаны в справочной системе (именно оттуда я взял функцию LargestPrimeGap), иногда требуют неоправданно большого объема памяти. Недостаточный объем памяти может помешать получить нужные результаты. Даже ночной прогон в таких случаях не помогает.
Давайте посмотрим, можно ли исправить ситуацию. Сначала загрузим пакет теории чисел.
<<NumberTheory`NumberTheoryFunctions`Теперь определим функцию LargestPrimeGap01.
LargestPrimeGap01[n_] := Block[{p1 = 2, p2 = 3, i = 2, pk = PreviousPrime[n + 1], d = Max[n - pk, 1]}, While[p2 < pk, { p1 = p2; p2 = NextPrime[p2]; delta = p2 - p1; If[delta > d, d = delta] }]; d]В определении этой функции мы воспользовались функцией previousPrime[n], которая генерирует наибольшее простое число, меньшее n, и функцией NextPrime[n], которая генерирует наименьшее простое число, большее n.
Вот небольшой тест.
LargestPrimeGap01[11] 4Этот тест функция выдержала. Теперь можем перейти к главному экзамену.
base=10; Do[Print[{n, LargestPrimeGap01[base ^ n]}}, {n, 2, 9}] {2.8} {3.20} {4.36} {5.72} {6.114} {7.154} {8.220} {9.282}На этот раз, как видите из рис. 5.4, загрузка ЦП не падает, и потому при нехватке дневного времени ночной прогон программы вполне может спасти ситуацию.
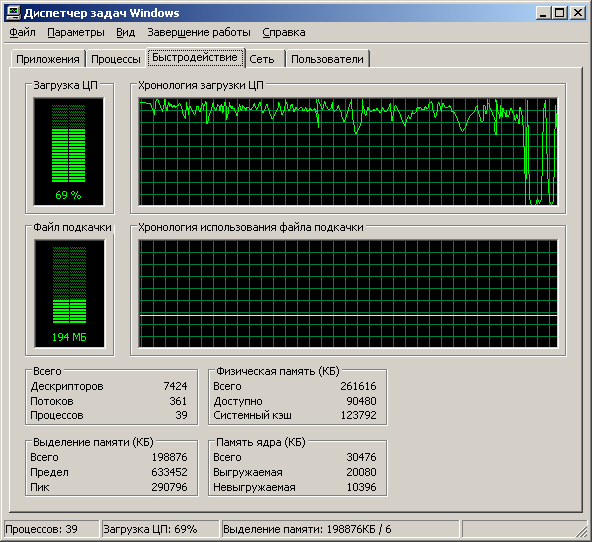
Рис. 5.4. Отчетливо видно, что файл подкачки не растет, а загрузка ЦП не падает ниже 50% несмотря ни на какие переключения задач
