Иллюстрированный самоучитель по Mathematica 5

Пифагоровы треугольники, у которых длины двух сторон выражаются простыми числами

Как известно, треугольники, у которых длины двух сторон выражаются целыми числами, называются пифагоровыми. Хорошо известно, что длина ни одной из сторон пифагорового треугольника не может быть равна 2. Поэтому у пифагоровых треугольников длины сторон могут выражаться только нечетными простыми числами. А потому длина хотя бы одной из сторон пифагорова треугольника должна быть четной (по теореме Пифагора) и потому выражается составным числом. (Составным потому, что четным, отличным от 2.) Боле того, несложно доказать, что если р и q – длины сторон пифагорова треугольника, выражающиеся простыми числами, то р² = 2q -1.

И наоборот, если существуют такие простые числа р и q, что р² = 2q -1, то в прямоугольном треугольнике с гипотенузой q и катетом р второй катет равен √q² -р² = q -1.

И потому такой треугольник будет пифагоровым. Для нахождения пифагоровых треугольников, у которых длины двух сторон выражаются простыми числами, можно применить функции PrimeQ и NextPrime. Область поиска ограничим теми треугольниками, у которых меньший катет р не превосходит заданного числа п. Достаточно найти длину меньшего катета р и длину гипотенузы q, поскольку длина второго катета на единицу меньше длины гипотенузы: q-1.

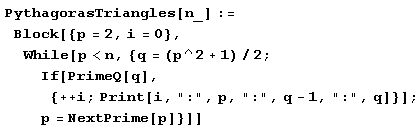
Порядок использования этой функции такой: сначала загрузить пакет теории чисел, а затем ввести это определение. Только после этого можно ее вызвать.

Результаты удобно отформатировать в виде таблицы.

Как видно из таблицы, таких треугольников совсем немного. Интересно, сколько же таких треугольников, у которых длина меньшего катета выражается не более чем n-значным числом? Давайте посчитаем. Вот нужная нам функция, которая печатает свой аргумент п, двоеточие: и количество найденных ею треугольников, меньший катет которых не превосходит n.

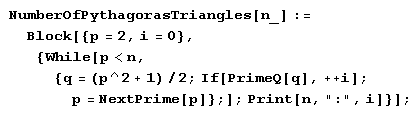
Теперь можем выполнить вычисления.

Результаты отформатируем в виде таблицы.