Иллюстрированный самоучитель по Mathematica 5

Линейное представление наибольшего общего делителя (функция ExtendedGCD)

Теперь выполним программу. Сколько раз сработала вспомогательная печать? Ни разу! Это значит, что по всем найденным значениям г и s можно восстановить многочлены г(х) и s(x) и написать тождество d(x) = r(x)a(x)+s(x)b(x)\ Полученные результаты стоят того, чтобы собрать их в таблицу (табл. Б.33).

Полученная таблица заслуживает более внимательного рассмотрения. Рассмотрим, например, одну строку таблицы.

Так как d(x) = xd -I = лс-1, эта строка означает, что х-1 = d(x) = r(x)a(x)+s(x)b(x), где а(х)= JC20-1, 'b(х) = хⁿ -1, r(х) = 1+x³ +x⁶ +х⁹ +x¹² +x¹⁵, s(x) =-(х+х³ + х⁶ +x⁹ +х¹² + х¹⁵ +х¹⁸). Иными словами, она означает, что х-1 = d(x) =r(х) (х²⁰ – 1) +s(x) (хⁿ – 1) для указанных только что полиномов г(х) и s(x).

Впрочем, вместо r(x) и s(x) можно подставить их выражения, и тогда получится следующее тождество:

X-1 = (1+х³ +x⁶ +x⁹ +x¹² +x¹⁵) (х²⁰ -1) – (х+х³ + х⁶ +х⁹ + х¹² +х¹⁵ +х¹⁸) (х¹⁷ -1).

Таким образом, мы видим, что каждая строка полученной таблицы фактически основана на полиномиальном тождестве и фактически является кратким его кодом!

Давайте теперь сравним полученные значения для г и s в равенстве НОД(a, b) = ra+sb для а = х^n-1 -1, b= х^m+1 -1 (х целое) с теми, которые были получены ранее для такого же равенства для чисел а и b, десятичная запись которых состоит из т единиц и n единиц. (Нужную таблицу мы подготовили заранее.) Не случайно ли значения г и s совпадают? Нет, не случайно.

Дело в том, что если справедливо равенство НОД(а, -b) = ra+sb для а = х^n-1 -1, b = x^m+1 -1 (х целое, отличное от 1), то справедливо и равенство 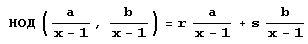потому что 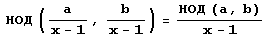. (Напомню, что числа 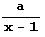и 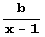целые при целом х и а = хⁿ⁺¹ -1, b = x^m+1 -1.) Более того, запись чисел 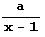и 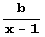в системе счисления с целым основанием х как раз и состоит из n единиц и m единиц.

Поскольку равенства НОД(а, b) = ra+sb и 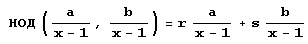для а= xⁿ⁺¹ -1, b= х^m+1 -1 (х целое, отличное от 1) равносильны, то г и s принимают в них одинаковые значения. Отсюда, в частности, следует, что если числа r и s из равенства НОД(а,b) = ra+sb имели одно и то же представление для любого основания системы счисления х, то же самое будет справедливо и для чисел r и s из равенства 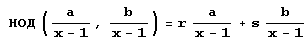, потому что значения r и s в этих равенствах одинаковы!

Это немного неожиданно, потому что сами значения а = xⁿ⁺¹ -1, b= х^m+1 -1, 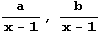, r и s зависят от основания системы счисления xl. Эта независимость как раз и является следствием полиномиальных тождеств. Причем тождества, получаемые для чисел, десятичная запись которых состоит из m единиц и n единиц, и тождества, получаемые для чисел а = хⁿ⁺¹ -1 и b = x^m+1 -1, фактически отличаются только множителем х-1. Например, из тождества x-1 = (1+х³ +x⁶ +x⁹ +x¹² +x¹⁵) (х²⁰ -1) – (х+х³ + х⁶ +х⁹ + х¹² +х¹⁵ +х¹⁸) (х¹⁷ -1), получается еще более длинное тождество:

1 =x-1 = (1+х³ +x⁶ +x⁹ +x¹² +x¹⁵) (х²⁰ -1) – (х¹⁹ + х¹⁸ +х¹⁷ +…+х+1) – (1+х³ +x⁶ +x⁹ +x¹² +x¹⁵ +x¹⁸) *(х¹⁶ + х¹⁵ +х¹⁴ +…+х+1).

Обратите, наконец, внимание на то, что в полученной таблице представления чисел r и s содержат только нули и единицы. Это означает, что коэффициенты полиномов r(х) и s(x), построенных по представлениям чисел r и s, тоже будут равны 0 и 1 (либо -1, если перед представлением стоит знак минус).