Иллюстрированный самоучитель по Mathematica 5 › Модулярная арифметика: деление с остатком, вычеты, сравнения и китайская теорема об остатках › Деление с остатком. Частное при делении с остатком (функция Quotient). [страница - 145] | Самоучители по математическим пакетам

Иллюстрированный самоучитель по Mathematica 5

Деление с остатком. Частное при делении с остатком (функция Quotient).

При выполнении операции деления с остатком получается частное и остаток. Для нахождения частного и остатка в системе Mathematica предусмотрены функции Quotient и Mod.

Чтобы получить частное при делении (с остатком) л на т, нужно воспользоваться функцией Quotient [n,m]. Рассмотрим пример.

Quotient[16.5]  
3

Для целых n и m выражение Quotient [n,m] равносильно Floor [m/n]. Однако n и т могут быть вещественными и даже комплексными числами.

Quotient[E ^ 10, E ^ 8]  
7 
Quotient[E ^ 10 + 25 * 1, E ^ 8 + 41]  
7 - 1

В случае вещественных чисел Quotient [n, m] – это такое целое число х, что d<n-m х<d+m. Однако часто нужно найти целое число х, такое, что d<n-m x<d+m. Пожалуйста, укажите сдвиг d третьим параметром.

Quotient[16.5.14] 
0

Вот как можно найти частные от деления чисел 0, 1, 2,…, 21 на 3.

Quotient[Range[0.21], 3]  
{0.0.0.1.1.1.2.2.2.3.3.3.4.4.4.5.5.5.6.6.6.7}

А вот частные, когда задан сдвиг 1.

Quotient[Range[0.21], 3.1] 
{-1.0.0.0.1.1.1.2.2.2.3.3.3.4.4.4.5.5.5.6.6.6}

А вот частные, когда задан сдвиг 2.

Quotient[Range[0.21], 3.2] 
{1.-1.0.0.0.1.1.1.2.2.2.3.3.3.4.4.4.5.5.5.6.6}

Пример 7.1. Графики функции Quotient.

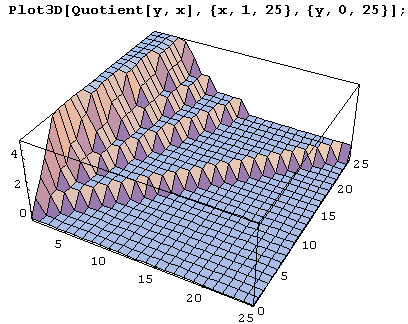
Давайте теперь построим несколько графиков функции Quotient. Поскольку это функция двух аргументов, построим изображения поверхности z = Quotient [х, у]. Для этого используем функцию plot3D.

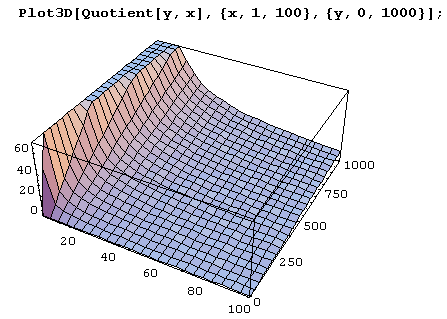
Иллюстрированный самоучитель по Mathematica 5 › Модулярная арифметика: деление с остатком, вычеты, сравнения и китайская теорема об остатках › Деление с остатком. Частное при делении с остатком (функция Quotient).

А вот вид вблизи.