Иллюстрированный самоучитель по Mathematica 5

Китайская теорема об остатках (функция ChineseRemainder)

Хитрый китаец Сунь Цю около 2000 лет назад (конечно, это могло быть и 200 лет до нашей эры, и 200 лет после начала нашей эры) открыл правило "гай-йен" ("большое обобщение"), которое является частным случаем целочисленного аналога интерполяционной формулы Лагранжа для полиномов. (Правда, примерно в то же самое время, в 100 г. н. э., греческий математик Никомах знал точно тот же частный случай.) Полностью формула была сформулирована и доказана впервые, по-видимому, в 1734 году Л. Эйлером. Сформулируем китайскую (или греко-китайскую, как назвал ее Акритас, автор одного из широко известных учебников по компьютерной алгебре?) теорему об остатках и укажем соответствующее правило (формулу).

Пусть m₁, m₂,…, m_r – попарно взаимно простые модули (попарно взаимно простые положительные целые числа), m = m₁, m₂,… m_r – их произведение, а а, u₁, u₂,…, u_r – произвольные целые числа. Тогда существует ровно одно целое число и, такое, что а<u<а+m, удовлетворяющее всем сравнениям u = u_i(modm_i). Более того:

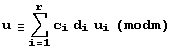
Где c_i – произведение всех модулей, кроме m_i: с_i = m/m_i, a _di=c_i^-1 (modm_i) (т.е .d_ic_i = 1(modm_i)).

Эта теорема имеет многочисленные применения в математике, информатике (машинная арифметика) и криптологии (секретные ключи). Для нахождения числа и, существование которого гарантировал хитрый китаец Сунь Цю, в пакете теории чисел существует "китайская" функция ChineseRemainder. ChineseRemainder [список_1, список_2] – это такое наименьшее целое неотрицательное число и, что Mod [и, список_2] = список_1. Чтобы ею воспользоваться, нужно сначала загрузить пакет теории чисел.

После загрузки пакета можно вызвать эту функцию.

Полученный ответ означает, что 244=0(mod4), 244=1(mod19) и 244=2(mod121). С помощью функции Mod это легко проверить.

Пример 7.5. "Задача о корзинке с яйцами".

Есть одна очень старая задача, в которой используется китайская теорема об остатках. Вот современная формулировка задачи. Крестьянка (наверняка отличница местной школы, а может даже победительница олимпиад по поднятию тяжестей) несла по проселочной дороге на базар яйца. Однако по дороге очень быстро ехал экипаж с сеньором, и экипаж нечаянно зацепил корзинку, в которой были яйца. Корзинка опрокинулась, и яйца разбились. Сеньор пожелал возместить убытки и спросил, сколько яиц было в корзинке. Крестьянка ответила, что не помнит, однако вспомнила, что когда вынимала яйца парами, то оставалось одно яйцо, когда тройками, то – два яйца, когда семерками – то 6 яиц и, вообще, когда она вынимала по p_i (p_i -i-e простое число) яиц, то в корзинке оставалось ровно i яиц. И еще вспомнила, что так она делала для всех первых ста простых чисел. Спрашивается, какое наименьшее число яиц могло быть в корзинке. С помощью функции ChineseRemainder это число можно найти так.

Ну и корзинка, которая вмещала столько яиц!