Остаток от деления (функция Mod)
Ниже приведены основные свойства функций Quotient и Mod:
- n*Quotient[m, n, d] + Mod[m, n, d] = m при любых допустимых m, n, d;
- знак Mod [m, n] совпадает со знаком и при любых допустимых вещественных m, n;
- Mod[m, n] = m-n*Quotient [m, n] при любых допустимых m, n;
- Mod [m, n, d] = m-n*Quotient [т, n, d] при любых допустимых m, n, d;
- Mod[x, 1] равно дробной части х
Ну и, наконец, полезно иметь в виду, что аргументы функции Mod могут быть списками. Это, например, позволяет найти остаток от деления данного числа сразу на несколько чисел.
Mod[244, {4, 9, 121}] {0.1.2}Можно также найти остатки от деления нескольких чисел на заданное число.
Mod[{0,1,2.3.4}2.5] {0.1.4.4.1}Пример 7.2. Графики функции Mod.
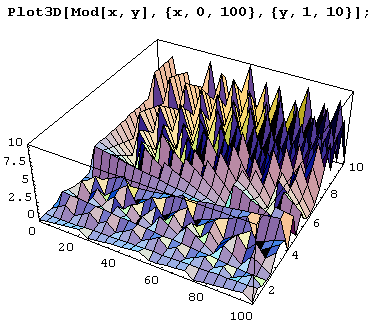
Теперь давайте построим несколько графиков функции Mod. Поскольку это функция двух аргументов, построим изображения поверхности z = Mod[x, у]. Для этого используем функцию Plot3D.
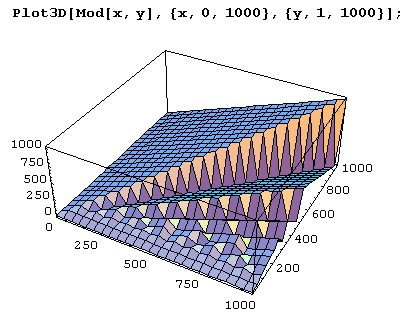
А вот вид вблизи.