Наименьшее общее кратное (функция LCM)
Пример 6.12. Графики функции LCM.
Давайте теперь построим несколько графиков функции LCM. Поскольку это функция двух аргументов, построим изображения поверхности:
z = LCM[IntegerPart[x], IntegerPart[y]]Для этого используем функцию Plot3D.
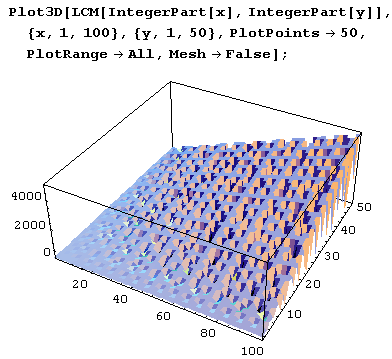
А вот вид вблизи.
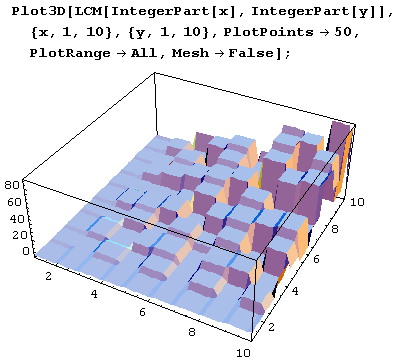
Резюме
Задача нахождения наибольшего общего делителя и наименьшего общего кратного нескольких чисел столь важна, что ее приходится решать практически постоянно. Даже занимаясь решением задач вариационного исчисления, математической физики, линейной алгебры, математического анализа, аналитической геометрии или просто решая какие-нибудь дифференциальные уравнения, вам практически не удастся избежать сложения или вычитания дробей – действий, которым учатся в пятом классе. И как только вам приходится выполнять эти действия, вы так или иначе вспоминаете о наибольшем общем делителе и наименьшем общем кратном. К счастью, система Mathematica если и не позволяет забыть об этих двух важнейших понятиях арифметики, то избавляет вас от рутинной работы по их нахождению.
В системе Mathematica реализованы весьма эффективные, вполне современные алгоритмы нахождения наибольшего общего делителя и наименьшего общего кратного. Пользуясь ими, вы можете быть уверены, что используете самые современные инструменты. Конечно, их применение целиком зависит от вас. Вы можете составить таблицы, найти тождества, решить неопределенные уравнения…
