Возведение в степень в модулярной арифметике (функция Power Mod)
Почти так же можно вычислить и последнюю тысячу знаков.
Mod[9^(9^9), 10^1000] //Timing{260.64 Second, 16437894757477844731142780767037267003263590250822342923877464623911279751529028988405927046285969119001418842032015433264756391857718597649 2049122303238110272101369183684943285741373762637969125845614123744406 0102002608592235410622770718702230402359356419151296996286668460066302 9835137902721579657456534443278490334199454357557541697596627896410612 70387990256128353667950589936117172490285814571733915187602283281383558665788995350272253954345165983917336427507154331749386377957650223307 1689586371971921105787378573369432124577155212755139983177854767167859 1299645067296274837365302215234320507478340927905653712738326405359097 6996351343597753799283680752817548382724478144536940979972304718417625 8944795154018072624283659761429188348967918815377285476781074966161266185476266685323552900557188849167988554700684735826850897391870085107540281885392534905291228820397197240322357870060732838773582826170043150602250406601961656994397543610268552663740366829061901749234943241787 99359681422627177289}Вычисление, как видите, заняло более четырех минут (260.64 секунды). Но гораздо быстрее результат можно получить вот так.
PowerMod[9.9^9, 10^1000] //Timing {0.015 Second, 1643789475747784473114278076703726700...2627177289}(Здесь середина пропущена.) Это вычисление заняло лишь 0.015 секунды. Это более чем в тысячу (точнее, в 17376) раз быстрее!
Пример 7.4. Графики функции Power Mod.
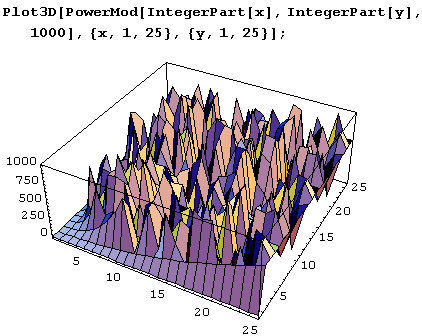
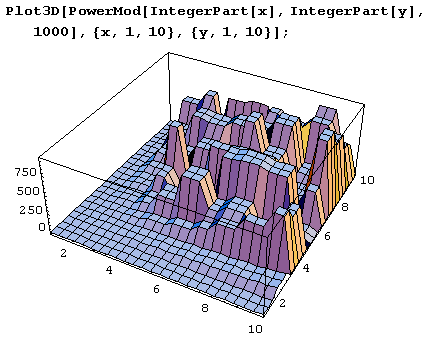
Давайте теперь построим несколько графиков функции PowerMod. Поскольку это функция двух аргументов, построим изображения поверхности z = PowerMod[x, у]. Для этого используем функцию Plot3D.
А вот вид издалека.