Корни в системе остаточных классов. Квадратный корень по модулю (функции SqrtMod и SqrtModList).
Список всех квадратных корней по модулю – функция SqrtModList
Как мы только что видели, квадратных корней может не быть совсем, а может быть несколько. Список всех квадратных корней из данного числа по заданному модулю дает функция SqrtModList. Если квадратных корней нет, список, естественно, будет пустым. Вот пример, когда существует два квадратных корня.
SqrtModList[3.11] {5.6}А вот пример, когда квадратных корней нет совсем.
SqrtModList[2.11] {}Существование квадратного корня по модулю и символ Якоби – функция JacobiSymbol
Как узнать, существует ли квадратный корень из данного числа d по модулю n? Иногда для этого достаточно вычислить символ Якоби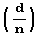 
. Если символ Якоби 
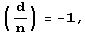го d является квадратичным невычетом по модулю d.
Если же Якоби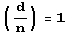 
и и простое, то d является квадратичным вычетом по модулю п. (Однако если неизвестно, простое ли п, но известно, что символ Якоби 
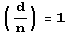то о квадратично сти вычета d по модулю и судить непосредственно нельзя.) Для вычисления символа Якоби в системе Mathematica предусмотрена функция JacobiSymbol [d, n]. Число 2 не является квадратичным вычетом по модулю 13, а число 4 является таковым (по любому модулю).
{JacobiSymbol[2.13], JacobiSymbol[4.13]} {-1.1}