Простые числа вида k * 2 n +1
Эта программа существенно быстрее первоначальной, но если хотите по ней найти n = 20 909, понадобится время и ангельское терпение.
Как видим, предварительная отбраковка и в данном случае значительно повышает эффективность программы. Впрочем, эффективность программы все еще сильно определяется неотсеянными показателями n, кратными 4. Хотелось бы и для них найти такое основание а, чтобы для установления простоты числа 3*2n +1 достаточно было проверить выполнение сравнения ат k =-1 (mod /a2n +l). (Ранее для показателей n, не кратных 4, мы полагали а = 5.)
Но все дело в том, что если показатель п делится на 4, то выбрать основание а несколько сложнее. Если показатель п делится на 4, в качестве основания а можно взять любой квадратичный невычет г по модулю 3 * 2n +1. Поэтому если п делится на 4, то сначала нужно найти (желательно небольшой) квадратичный невычет t по модулю 3*2n +1, а затем проверить, выполняется ли сравнение n2n-1 =-1(mod k*2n +l). Но как найти квадратичный вычет? Для этого можно использовать квадратичный закон взаимности.
Если Р>1 n Q>1 – положительные нечетные взаимно простые числа, то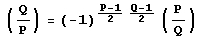 
Прежде всего заметим, что если Р – 3*2n +1, то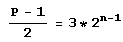 
– число, четное при n>1.
Поэтому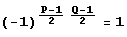 
и потому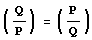 
Как видим, для поиска квадратичного невычета r можно использовать функцию JacobiSymbol. В качестве г можно брать небольшие нечетные числа и вычислять для них символ Якоби. (Для квадратичного невычета символ Якоби равен -1.) Как только мы найдем квадратичный невычет r, можем проверить, выполняется ли сравнение r2 k =-1 (mod 32n +l). Теперь легко написать функцию, вычисляющую квадратичный невычет.
MM3nr[nn_]: = Module[{r=5, JS=JacobiSymbol[5, nn]}, While[JS!=-1 && r<nn, r+=2; If[GCD[r,nn]= =1, JS=JacobiSymbol[r,nn]]];r]Чтобы запрограммировать критерий простоты, воспользуемся функцией PowerMod.
MMSnPrime[n_] := Module[{t = 3*2^n+1), If[Mod[n,4]!=0, PowerMod[5,(t-1)/2,t]==t-1, PowerMod[MM3nr[t],(t-1)/2,t]==t-1]]Теперь, наконец, можем написать окончательную версию программы.
M3nv01[n_] :=Block[{j=1, nnprime=25000,primen=Prime[nnprime], nn=Min[n,primen]}, While [MMkn[3,j]<= primen && j<=n, {If[MM3nPrime[j],Print[j]], J++H; If[j<n, t=Sort[DeleteCases[Array[f3,nnprime,3],Null]]; While[j<=nn, If[fx[j,t], If[MM3nPrime[j],Print[j]]];j++]]]Запуская программу с параметром nnprime = 10000 и 25000, убеждаемся, что при этих (и всех промежуточных) значениях генерация таблицы начинается после вывода показателя 12, но до вывода показателя 18. Затем программа довольно быстро добирается до показателя 3912, после вывода которого "уходит в себя" аж до вывода показателя 20 909. (Заметьте, что, в отличие от предыдущей версии программы, перерыв между показателями 534 и 2 208 не слишком заметен – эту "достопримечательность" вы запросто можете пропустить, если выйдете выпить чашечку кофе!)
Оказывается, что число 3*2n + 1 является простым при n = 1, 2, 5, 6, 8, 12, 18, 30, 36, 41, 66, 189, 201, 209, 276, 353, 408, 438, 534, 2 208, 2 816, 3 168, 3 189, 3 912, 20 909, 34 350, 42 294, 42 665, 44 685, 48 150, 55 182, 59 973, 80 190, 157 169, 213 321. При всех других n, не превосходящих 300 000, число 3*2n + 1 является составным.
Резюме
Мы рассмотрели определение частного (функция Quotient) и остатка (функция Mod), а также возведение в степень в модулярной арифметике (функция PowerMod) и основу основ модулярной арифметики – китайскую теорему об остатках (функция ChineseRemainder). Кроме того; мы затронули вопрос об извлечении квадратных корней (функции SqrtMod, SqrtModList и JacobiSymbol). Но мы не ограничились корнями второй степени, а научились находить первообразные корни по модулю n (функция PrimitiveRoot), а также показатели (функция MultiplicativeOrder). Как оказалось, некоторые из рассмотренных функций используют каноническое разложение (функцию Factorlnteger) и потому не могут справиться с вычислениями при очень больших аргументах. Однако на реальных примерах мы убедились в том, что эти функции очень полезны и вполне пригодны даже тогда, когда вычисления ведутся с очень большими числами, например с числами, близкими к тысячным, десятитысячным, стотысячным и даже миллионным степеням двойки.