Иллюстрированный самоучитель по Mathematica 5

Функция Эйлера (EulerPhi)

В чем же причина такого медленного продвижения, почему мы продвигаемся только на один шаг? Это происходит потому, что мы на самом деле устраняем быстрый рост функции nx = x(nf} только на последнем шаге. Почему это происходит? Потому, что мы все время связаны с определением функции GodF. Именно она используется внутри функции GodFLastk. Даже фактически отказавшись от явного применения функции GodFLastk, мы все равно стремимся записать выражение для nх = х(nⁿ) с некоторыми упрощениями для последнего или предпоследнего возведения в степень. Конечно, это так естественно использовать выражение для "х = х('). Однако нужно иметь в виду, что использование подобных "прямолинейных" определений часто весьма неэффективно. Если уж мы решили повышать эффективность, то делать это нужно на всю "глубину" выражения. Правда, это неизбежно приведет к появлению новых функций. Нам, например, придется отказаться от функции GodFLastk. Как ни удивительно, но вместо нее нам понадобится только одна функция, притом довольно простая. Давайте найдем ее определение. Обозначим через С(n, х, k) остаток от деления "х на k. (Таким образом, G(n, х, m) – это последние т цифр числа nх.) Тогда 0(1, х, k) = Mod [х, k]. С другой стороны:

Предположим теперь, что х и k взаимно просты. Тогда по малой теореме Ферма это выражение можно записать так: PowerMod [x, G(n, х, ср(А:)), k].

Так что в этом случае G(n+l, x, k) = PowerMod [x, G(n, x, <p(k)), k].

Это и есть нужное нам рекуррентное соотношение. С учетом этого соотношения определение нужной нам функции выглядит так.

Теперь легко написать программу.

Давайте теперь выполним аналогичные вычисления для числа 3. Вот так запишется программа.

Теперь понятно, что имел в виду Вальтер Литцман под аналогичными свойствами. Начиная с некоторого и = и" последняя цифра числа не изменяется, причем начиная с и = <<() + 1 повторяются уже две цифры, с n = n0+2 – три цифры, с n = n0+k – k цифр и т. д. (Через и" (х) удобно обозначать наименьшее п0 с таким свойством.) Для некоторых х, например для х = 9, n(х) = 1, а для некоторых х (n)>1. Если п0(х)>1, то нельзя утверждать, что последние n цифр числа "х повторяются во всех последующих числах "+1x, "+2х,… и т.д. Если п0(х)>1, то повторение последних n цифр начнется не с числа "х, а несколько позднее! Да уж, разбираться в популярных книжках иногда приходится с системой Mathematica.

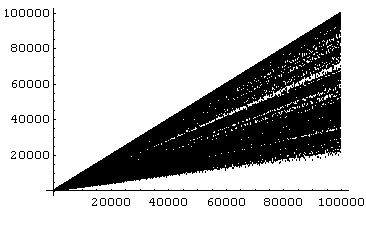
Пример 8.2. График функции Эйлера.

Давайте теперь построим график функции Эйлера. Сначала используем функции Table и EulerPhi для построения таблицы tl (точнее, списка) значений функции Эйлера.

Теперь можем использовать функцию ListPlot для построения графика.

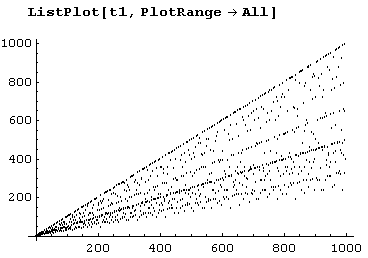
А вот график для n = 100000.