Функция Кармайкла (CarmichaelLambda)
Функция Кармайкла – λ(m).
Если а и т взаимно простые, то a4n-1 0 =}(modm). Но всегда ли φ(m) является наименьшим натуральным числом с таким свойством? Оказывается, нет. Например, для модуля 8 имеем следующую приведенную систему вычетов.
s=Select[Range[8],GCD[#,8]==!&] {1.3.5.7}Квадраты этих вычетов сравнимы с 1 по модулю 8.
Mod[%-2.8] {1.1,1.1}Однако:
EulerPhi[8] 4Так что φ(8) не является наименьшим натуральным числом, удовлетворяющим сравнению an =l(mod8) для всех а, взаимно простых с 8.
Значения, меньшие φ(n), иногда доставляет обобщенная функция Эйлера). Вдвое меньшие значения для модулей, кратных 8, дает функция Люка φ(x). А наименьшее натуральное число, удовлетворяющее сравнению аi =1 (mod от) для всех а, взаимно простых с т, обозначается N/n). Функция А. называется функцией Кармайкла. В системе Mathematica у нее имя CarmichaelLambda.
Вот как можно вывести те натуральные числа, для которых k(m)<<р(m).
Do[If[EulerPhi[n]!=CarmichaelLambda[n], Print[n,":",EulerPhi[n],":",CarmichaelLambda[n]]],{n,k=100}]Выполните эту программу, и вы увидите, что их довольно много.
Пример 8.3. График функции Кармайкла.
Давайте теперь построим график функции Кармайкла. Сначала мы используем функции Table и CarmichaelLambda для построения таблицы tl (точнее, списка) значений функции Кармайкла.
tl= Table[CarmichaelLambda[k], {k,1,n=10^3)];Теперь можем использовать функцию ListPlot для построения графика.
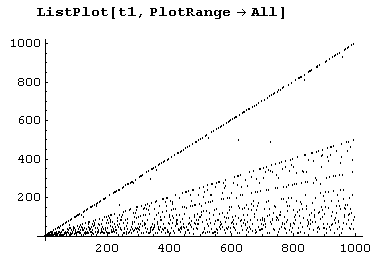
А вот график для n = 100000.
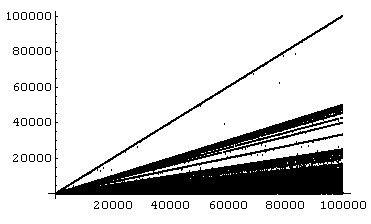
Сравните эти графики с графиками функции Эйлера. Сразу видно, что лучи на графике функции Кармайкла прижимаются к оси абсцисс гораздо ближе, чем на графике функции Эйлера.
