Иллюстрированный самоучитель по Mathematica 5

За гранью простого. Новый вид науки.

Значение х* может быть найдено из уравнения х* = f(x*).

Все точки, удовлетворяющие этому уравнению, являются неподвижными точками функции f, так как если х, = х', то и х2 = х', хn = х' при любом n.

При r<1 квадратное уравнение х=rх(1 – х) имеет один неотрицательный корень х=*0. При t › 1 неотрицательных корня два: х* = 0 nх* = (t-1)/r. При r= 1 происходит бифуркация: неподвижная точка х' = 0 теряет устойчивость, а вновь появившаяся точка становится устойчивой.

Можно довольно просто определить, будет ли устойчивой неподвижная точка х отображения f[x]. Пусть х" = х + Δхn, где Δхn – малое число. Если точка устойчива, то с ростом n величина |Δхn| должна уменьшаться. Перепишем формулу х_n+1 = f(xn, r) в виде:

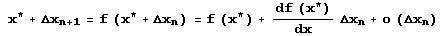
Если в последнем равенстве опустить член о(Δхn), то полученное приближенное равенство будет выполняться тем точнее, чем меньше Δхn (мы пренебрегли членами, пропорциональными (Δхn)², (Δхn)³ и т.д.). Поскольку x* = f(x), то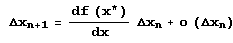

И для того чтобы Δх_n+1 › 0 при n › ∞, должно выполняться неравенство .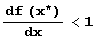

Это и есть условие устойчивости точки х*.

Будем дальше увеличивать параметр r. Поведение системы снова изменится: в последовательности {хn}, начиная с достаточно больших и, будут чередоваться числа, близкие к некоторым двум числам я, и а2. (Точнее говоря, последовательность устроена так, что x_2n+1 › a₁, х_2n+1 › n₂ при n › ∞) Эти числа связаны соотношениями а1 = f(а₂), а₂ = f(а₁). Иными словами, в этом случае отображение х_n+1 = rхn(1– хn) имеет устойчивый цикл с периодом 2. Обозначим этот цикл 52. Наличие цикла S* в нашей модели означает, что численность популяции будет меняться с периодом в 2 года.

Выясним, как выглядят циклы на графике. Для этого определим программу cobwebPlot.

Сначала протестируем эту программу.