За гранью простого. Новый вид науки.
Таким образом, переход от 51 к 52 в отображении f(x) обусловлен тем, что в отображении f (х) одна из неподвижных точек теряет устойчивость и в ее окрестности появляются две новые устойчивые неподвижные точки. Здесь вновь происходит бифуркация. Рассматривая функции f4 (х), fn (x) и так далее, можно посмотреть, как происходят следующие удвоения.
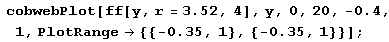
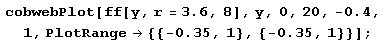
На примере модели хn+1 = rхn(1 -хn) можно понять не только качественные, но и удивительные количественные закономерности. Чтобы проследить за ними, построим график х(r): по оси х будем откладывать х1, х2,…, лежащие на устойчивом цикле, по оси г – значения параметра. Циклу S* будут соответствовать две точки на одной вертикали, циклу S1 – четыре и т.д. Тогда получим ранее приведенный график, отражающий усложнение устойчивых циклов в отображении хn+1 = rхn(1-хn), происходящее в результате бифуркаций удвоения периода.
Обозначим через R1, R2, R},… те значения параметра г, в которых происходили удвоения, а через r1, r2, г3,… – значения параметра, при которых х= 1/2 является элементом цикла S2, S4, Ss и т. д. Введем также величины d1, d2,…, dn,.., равные расстоянию между х = 1/2 и ближайшим к нему элементом цикла S2 при r = rn. Расчеты показали, что числа f(x) и rn при больших и ведут себя как геометрическая прогрессия со знаменателем a = 4.6692016… Другими словами,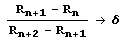 
и отношение dn/dn+1 также имеет предел, равный некоторому числу а, причем а = 2.5029078…
Что будет, если вместо функции хn+1 = rхn(1 -хn) взять любую другую симметричную функцию, которая имеет на отрезке [0, 1] один максимум и около вершины близка к квадратичной параболе. Пусть в ней также происходит бесконечная последовательность бифуркаций удвоения при изменении некоторого параметра. Оказалось, что в любой такой модели числа а и 5S будут одними и теми же! Более того, независимо от вида функции предел lim(-a)n f2n [(x-0.5)/(-a)n, rn] существует и будет одной и той же универсальной функцией, обозначаемой часто через g0(х).
Эти удивительные закономерности были обнаружены и поняты американским математиком М. Фейгенбаумом в 1978 году. В силу универсальности чисел а и 5 и функции g0(x), a также других функций такого типа эту теорию называют теорией универсальности.
Что же означают эти результаты?
В природе можно выделить два совершенно различных на первый взгляд типа явлений. Одни – регулярные и упорядоченные. Это большинство процессов, используемых в технике и технологии, процессы, в которых возникают структуры. Как правило, ход таких процессов можно предсказывать, зная управляющие ими законы.
Другие процессы – случайные, хаотические. К ним относится турбулентное движение жидкости, шумы в различных электронных системах и т.д. Они требуют другого, статистического описания, которое позволяет получить некоторые усредненные характеристики процессов. Такие явления также очень важны, но используются гораздо реже из-за их сложности и недостаточной изученности. В одних случаях турбулентное движение жидкости позволяет транспортировать уголь, руду и многое другое по трубам. В других – с турбулентными вихрями приходится бороться. Хорошо зная законы турбулентного движения, можно было бы строить более быстрые и экономичные суда и самолеты.
Теория Фейгенбаума приводит к парадоксальному выводу: между хаосом и порядком есть глубокая внутренняя связь. Непериодический, случайный процесс возникает как предел все более сложных структур (циклов S2n). Хаос возникает как сверхсложная организация (цикл S2)! Этот вывод является очень общим: он может относиться к моделям экологии, гидродинамике – к любым системам, где есть последовательность бифуркаций удвоения периода.
Возможно, вы подумали, что сложность взаимоотношений порядка и хаоса, имеющая место в данной модели, связана с участием вещественных чисел. Тогда вспомните график функции Эйлера, график количества единиц в двоичной записи целых чисел. На этих графиках, где нет ничего, кроме целых чисел, также наблюдается сложная картина чередования хаоса и циклов.
Еще более сложная.картина может наблюдаться в многомерном (например, в двухмерном) случае. Если модель к тому еще и дискретная, то можно говорить о клеточных автоматах.