Иллюстрированный самоучитель по Mathematica 5

За гранью простого. Новый вид науки.

Вот как все это выглядит на графике.

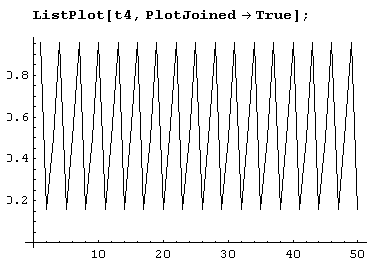
Вот теперь действительно есть чему удивиться! Численность популяции оказалась периодической функцией.

Конечно, здесь проведены вычисления только для r = 3.83, а нам нужно провести вычисления для разных r. Давайте проведем их для 250 значений г, равномерно распределенных между r = 2.8 и r = 4.0.

Здесь для каждого из 250 значений г строится список х_n для n – 101,…, 300. Вот что получается (конец опущен).

Чтобы построить график, этот список нужно сделать плоским:

Теперь список будет иметь вид (конец опущен):

И мы можем построить график, наглядно демонстрирующий поведение последовательности {*"} при различных значениях параметра г в отображении х_n+1= rх_n(1-х_n).

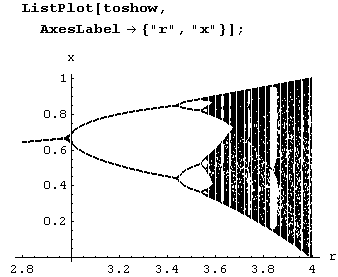
Из графика видно, насколько сложно зависит поведение популяции от r.