За гранью простого. Новый вид науки.
Еще раз обратим внимание на простенькую формулу хn+1 = rхn(1-хn). При небольших г (0<r<1) хn стремится к нулю независимо от выбора XQ. Судя по формуле хn+1= rxn(1-хn), вид, численность которого вначале равна XQ, выжить не может, сколько бы животных ни было вначале. Поведение последовательности в этом и в других случаях удобно представлять графически. Нарисуем кривую y=f(x) при заданном значении г и прямую у = х. Отложим х по оси абсцисс, проведем вертикаль до пересечения с кривой у -/(х) (точка А), а затем из точки пересечения горизонталь до пересечения с линией у = х (точка В). Теперь вновь проведем вертикаль до пересечения с кривой у = f(x), что даст нам точку С с координатой х2. Тогда х2 =f(х1). Взяв точку х2 за начальную и повторив все те же операции, получим х3, затем х4 и т.д.

Теперь рисуем график, чтобы представить поведение последовательности хn при n › ∞.
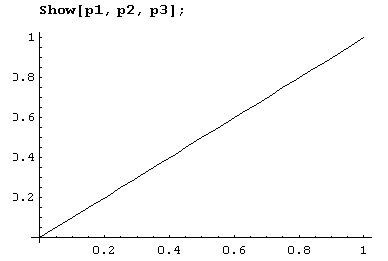
Из рисунка видно, что хn › 0 при n › ∞.
Из формулы хn+1 = rхn(1-хn) следует, что функция f(x) переводит отрезок [0, 1] в отрезок [0, r/4]. Если r<4, то все значения х" лежат на отрезке [0, 1] при условии, что 0<х<1. Так что формула хn+1 = rхn(1 -хn) задает отображение отрезка [=, 1] в себя.
Пусть теперь r немного больше 1, например r = 2.
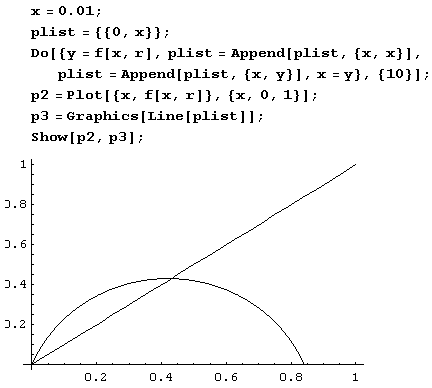
Видим, что при этом значении г последовательность {хn} ведет себя по-другому: хn стремится к постоянному, отличному от нуля, значению хn при n › ∞. В применении к исходной биологической задаче это означает, что численность такого вида по прошествии нескольких лет стабилизируется и перестанет меняться со временем.
