Иллюстрированный самоучитель по Mathematica 5

Системы дифференциальных уравнений

Функция DSolve позволяет также решать системы дифференциальных уравнений.

Пример 10.9.
Найдем решение системы дифференциальных уравнений х' = у, у' = -а² х, удовлетворяющее начальным условиям х = 1, у' = 0 при t = 0.

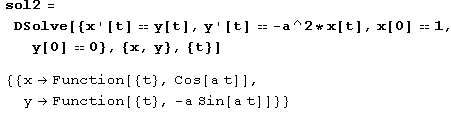
Теперь построим графики функций x(t) и y(t) для случая, когда параметр а принимает значение 1/2.

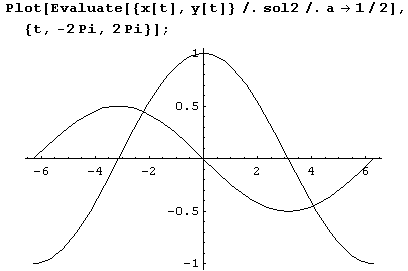
Чтобы построить фазовый портрет, нужно воспользоваться функцией ParametricPlot.

Однако не всегда функция DSolve справляется с системами дифференциальных уравнений.

Пример 10.10.
Найдем решение системы дифференциальных уравнений у"= y² +z, z'= -2yy'+y, удовлетворяющее начальным условиям у = 0, у'= 0, z = 0 при х = 0.

Как видите, несмотря на то что в данном случае решением является пара функций у = е*, z -ef -e1*, функция DSolve не смогла найти его. В таких случаях, как и одно дифференциальное уравнение, так и систему дифференциальных уравнений приходится решать численно.

Для этого можно воспользоваться функцией NDSolve. Вызов ее отличается от вызова функции DSolve лишь тем, что в нем нужно указать интервал, на котором ищется решение.

В данном случае уравнения представлены в виде интерполяционных функций для у(х) и z(x) на интервале (0, 10). Хотя это и не аналитические выражения, они позволяют вычислить значения наших функций – решений системы дифференциальных уравнений – в любой точке интервала (0, 10).