Дифференциальные уравнения. Поля направлений для дифференциальных уравнений и изоклины.
Чтобы представить поведение интегральных кривых дифференциального уравнения, полезно начертить поле направлений для данного дифференциального уравнения и изоклины – кривые, пересекающие интегральные кривые под заданным углом.
Построение поля направлений для дифференциального уравнения
Давайте применим теперь средства изображения векторных полей для рисования полей направлений для дифференциальных уравнений. Если дифференциальное уравнение первого порядка разрешено относительно производной, т.е. имеет вид y' = f(x, у), то поле направлении для него строится очень просто, нужно лишь в каждой точке (х, у) задать единичный вектор, коллинеарный вектору (1, f(x, у)). Иными словами, достаточно нормировать вектор (1,f(x, у)).
Пример 10.2.
Нарисуем поле направлений для дифференциального уравнения.

Совсем несложно начертить и изоклины интегральных кривых дифференциального уравнения первого порядка, разрешенного относительно производной, т.е. имеющего вид. у'= Аf(x, у).
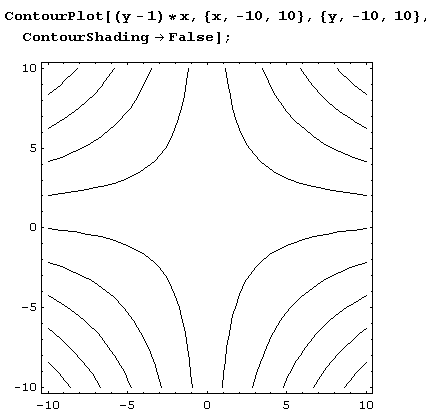
Построение изоклин интегральных кривых дифференциального уравнения
Если дифференциальное уравнение первого порядка разрешено относительно производной, т.е. задано в виде у'= f(x, у), то изоклины являются линиями уровня f(x, у) = С. Следовательно, задача построения изоклин сводится к построению линий уровня.
Пример 10.3.
Построим изоклины уравнения у'= (у-1)х.
Чертежи полей направлений и изоклин, несомненно, дают весьма хорошее представление об интегральных кривых. Однако куда важнее то, что система Mathematica может интегрировать дифференциальные уравнения!
