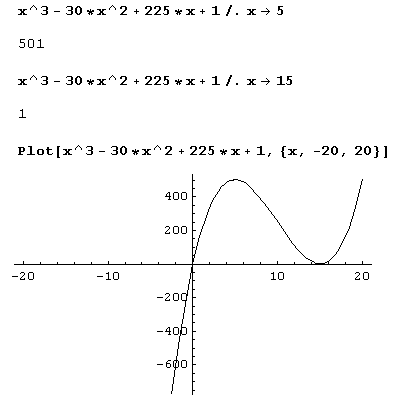Исследование функций и построение графиков
Едва ли можно указать единую схему, пригодную для исследования абсолютно всех функций. Так что едва ли стоит удивляться, что в курсах анализа можно найти множество таких схем – от совсем кратких, похожих на весьма общие указания, до обширных, развернутых, с множеством всевозможных пунктов, в большинстве своем не имеющим никакого отношения к конкретной исследуемой функции. Однако все такие схемы обычно имеют несколько общих пунктов.
Определение интервалов возрастания и убывания функции
Найдем для примера интервалы возрастания и убывания функции у = x3 -30x2 +225x+l. Сначала определим функцию.
У=х^3-30*х^2+225*х+1
1 + 225 х – 30 х2 + х3.
Данная функция – многочлен, поэтому она всюду дифференцируема. Найдем ее производную.
D[y,x] 225-60 х + 3х2.
Так как и производная – многочлен, разложим его на множители.
Factor[%] 3 (-15+x) (-5+x)Теперь видим, что производная отрицательна только на интервале (5; 15). На этом интервале функция, следовательно, строго убывает. На интервалах (-∞, 5) и (15, ∞) производная положительна. Поэтому на этих интервалах функция строго возрастает.
Нахождение локальных экстремумов
У рассмотренной нами функции у = х3-30x2 +225с+1 производная обращается в нуль в точках х= 5 и х= 15. Поскольку это простые нули производной, то именно эти точки и являются точками ее локального экстремума.
Легко вычислить значения функции в этих точках и построить ее график.