Интегрирование
Пример 10.1.
Вычислим моменты инерции относительно осей координат 0х и 0у пластины с плотностью 1, ограниченной кривыми ху = 1, ху = 2, у = 2х, х = 2у и расположенной в I квадранте.
Нарисуем пластину.
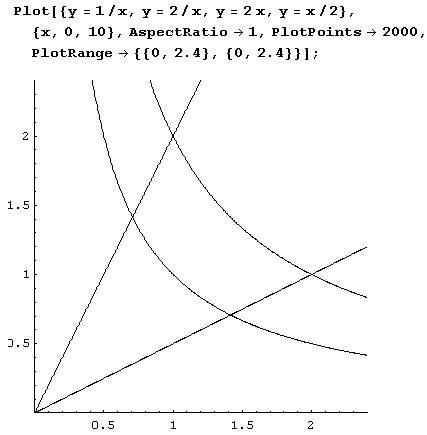
Теперь нужно вычислить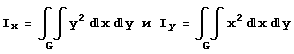 
где G – пластина.
Чтобы свести эти интегралы к повторным, перейдем к полярным координатам. Тогда пластина будет ограничена лучами φ1 = arctg 0.5 и φ2 = arctg 2 и кривыми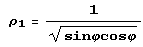 
(значение р на гиперболе ху = 1) и 
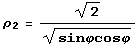(значение р на гиперболе ху = 2).
Поэтому далее мы бы написали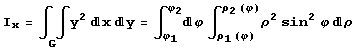 
и вычислили бы этот интеграл обычным путем.
Но с помощью системы Mathematica все можно сделать проще:
Момент инерции относительно оси 0у можно вычислить точно таким же методом. Впрочем, очевидно, что момент инерции относительно оси 0у равен моменту инерции относительно оси Ох.