Исследование функций и построение графиков
Вот более сложный пример. Пусть нужно найти локальные экстремумы функции 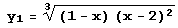 .
.
Определим нашу функцию в системе Mathematica.
Y1=((1-x) (х-2)^2)^(1/3)
((1-х) (-2 + х)2)1/3.
Данная функция определена и непрерывна на всей числовой оси. Находим ее производную.
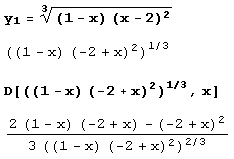
Видим, что производную можно упростить, поэтому применяем функцию FullSimplify. (Вообще говоря, это лучше делать всякий раз, когда вычисляются производные.)
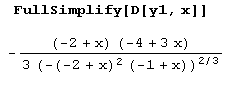
Видим, что в точках х = 1 и х = 2 производная не существует, а в нуль обращается только в точке х = 4/3. Поэтому только эти точки и являются критическими для данной функции. Однако при переходе через точку х – \ производная не меняет знака, поэтому она не является точкой экстремума. При переходе через точку х = 4/3 производная меняет знак минус на плюс, поэтому в этой точке функция имеет минимум. При переходе через точку х = 2 производная меняет знак плюс на минус, поэтому в этой точке функция имеет максимум. Вычисляем минимум и максимум.
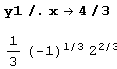
Так что локальный минимум равен 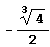 .
.
Точно так же вычисляется и локальный максимум.
y1/.x > 20Вот график данной функции.
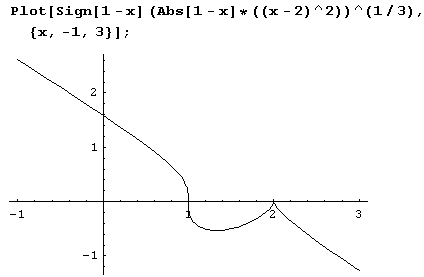
Заметьте, что для построения графика знак подкоренного выражения пришлось вынести из под корня, благодаря чему подкоренное выражение оказалось неотрицательным.
